
Скачай приложение iTest
Готовься к школьным экзаменам в более удобном формате
Квадратичная функция и ее свойства
Квадратичная функция – это функция вида \(y=a{{x}^{2}}+bx+c\), где \(a\ne 0, b \ и\ c\) – любые числа (они и называются коэффициентами). Число \(a\) называют старшим или первым коэффициентом такой функции, \(b\) – вторым коэффициентом, а \(c\) – свободным членом.
\(y=ax^2+bx+c=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}.\)
Графиком квадратичной функции является парабола, вершина которой находится в точке \((-\frac{b}{2a};-\frac{b^2-4ac}{4a})\).
Свойства квадратичной функции
- Область определения функции – вся числовая прямая: \(D(f) = R = (−∞; ∞)\).
- Область значений функции зависит от знака коэффициента \(a\). При \(a > 0\) ветви параболы направлены вверх, функция имеет наименьшее \((y_{min})\), но не имеет наибольшего значения: \(E(f) = [ y_{min}; +∞)\); при \(a < 0\) ветви параболы направлены вниз, функция имеет наибольшее \((y_{max})\), но не имеет наименьшего значения: \(E(f) = (−∞; y_{max} ]\).
- В общем случае функция \(y = ax^2 + bx + c\) не является ни четной, ни нечетной. Осью симметрии параболы является прямая \(x=-\frac{b}{2a}\). Функция будет четной только в случае, когда эта прямая совпадает с осью OY, т. е. при \(b = 0\).
- При \(a > 0 \) функция монотонно убывает на промежутке \((−∞; −\frac{b}{2a})\) и монотонно возрастает на промежутке \((−\frac{b}{2a}; +∞)\). При \(a < 0\) функция монотонно возрастает на промежутке \((−∞; −\frac{b}{2a})\) и монотонно убывает на промежутке \((−\frac{b}{2a}; +∞)\).
- Функция непрерывна на всей области определения.
- Асимптот не имеет.
- Парабола пересекает ось ординат в точке \((0;c)\). Если квадратный трехчлен имеет действительные корни \(x_1 ≠ x_2\), то парабола пересекает ось абсцисс в точках \((x_1;0)\) и \((x_2;0)\). При \(x_1 = x_2\) парабола касается оси абсциcс в точке \((x_1;0)\).
Зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции:
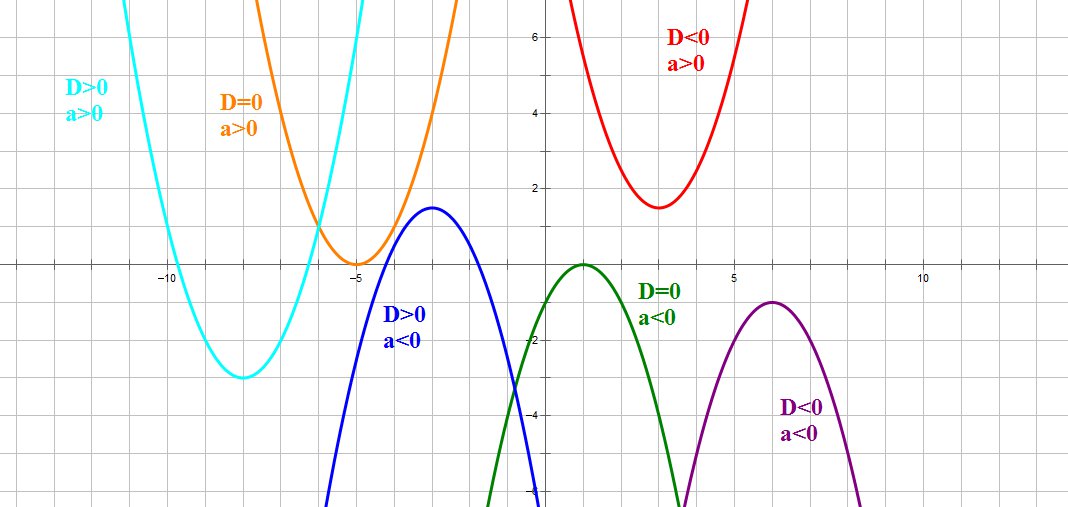
-
Найдите множество значений функции.
\(y=x^2-8x+9\)
-
Найдите область значений функции.
\(y=-x^2+2x+7\)





