Решение квадратных неравенств с помощью графика

Квадратным неравенством называют неравенство вида \(ax^2 + bx + c> 0\), где (вместо знака > может быть, разумеется, любой другой знак неравенства).

При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения \(ax^2+bx+c=0\). Для этого необходимо найти дискриминант данного квадратного уравнения. Можно получить 3 случая:

1) D = 0, квадратное уравнение имеет один корень;

2) D > 0, квадратное уравнение имеет два корня;

3) D < 0, квадратное уравнение не имеет корней.

В зависимости от полученных корней и знака коэффициента \(a\) возможно одно из шести расположений графика функции \(y=ax^2+bx+c\):

Если требуется найти числовой промежуток, на котором квадратный трехчлен \(ax^2+bx+c\) больше нуля, то этот числовой промежуток находится там, где парабола лежит выше оси ОХ.

Если требуется найти числовой промежуток, на котором квадратный трехчлен \(ax^2+bx+c\) меньше нуля, то этот числовой промежуток расположен там, где парабола лежит ниже оси ОХ.

Если квадратное неравенство нестрогое, то корни входят в числовой промежуток, если строгое – не входят.

Такой метод решения квадратного неравенства называется графическим.

Пример 1. Решить \(x^2–15x+50 > 0\).

Решаем квадратное уравнение \(x^2–15x+50=0\).

\(D = b^2–4ac = (–15)2–4\cdot1\cdot50 = 225–200 = 25\).

Находим корни:

\(\begin{aligned} x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-(-15)+5}2=\frac{20}2=10 \\x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-(-15)-5}2=\frac{10}2=5 \end{aligned}\)

Строим ось OX. Отметим полученные корни. Так как неравенство у нас строгое, то заштриховывать их не будем. Схематично строим параболу, расположена она ветвями вверх, так как коэффициент при х² положительный:

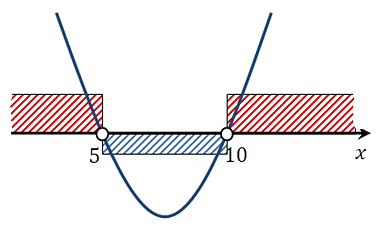
Определяем визуально положительные и отрицательные области, здесь мы их отметили разными цветами для наглядности, можно этого и не делать. Записываем ответ: \(x\in(-\infty; 5)\cup(10; +\infty)\).

*Знак U обозначает объединение решений. Образно можно выразиться так: решением является «этот» и « еще этот» интервал.

Пример 2. Решить: \(–x^2+x+20 ≤ 0\).

Решаем квадратное уравнение \(–x^2+x+20=0\).

\(D = b^2–4ac = 12–4\cdot(–1)\cdot20 = 1+80 = 81\).

Находим корни:

\(\begin{aligned} x_1=\frac{-b+\sqrt{D}}{2a}=\frac{-1+9}{2\cdot(-1)}=\frac{8}{-2}=-4 \\[6pt]x_2=\frac{-b-\sqrt{D}}{2a}=\frac{-1-9}{2\cdot(-1)}=\frac{-10}{-2}=5. \end{aligned}\)

Строим ось OX. Отметим полученные корни. Так как неравенство у нас нестрогое, то заштрихуем обозначения корней. Схематично строим параболу, расположена она ветвями вниз, так как коэффициент при х² отрицательный (он равен –1):

Определяем визуально положительные и отрицательные области. Сопоставляем с исходным неравенством (знак у нас ≤ 0). Неравенство будет верно при х ≤ – 4 и х ≥ 5. Записываем ответ: \(x\in(-\infty;-4]\cup[5;+\infty)\).

*Указаны квадратные скобки – это обозначает, что границы интервала входят в решение. Ось OY мы на эскизах не указали, так как она в данной ситуации не играет никакой роли, то есть при построении эскиза ось OY строить необязательно.