Определенный интеграл

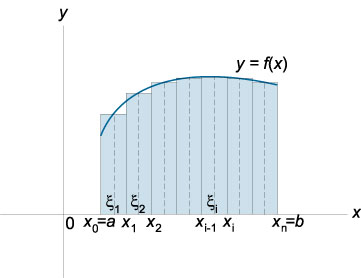
Определенным интегралом от функции \(f(x)\) на отрезке \([a;b]\) называется предел интегральной суммы при стремлении максимальной длины частичного интервала к нулю.

\(\require{AMSmath.js}\large\int\limits_a^b\normalsize {f\left( x \right)dx} = \lim\limits_{\substack{ n \to \infty\\ \text{max}\,\Delta {x_i} \to 0}} \sum\limits_{i = 1}^n {f\left( {{\xi _i}} \right)\Delta {x_i}} , \text{где}\;\;\Delta {x_i} = {x_i} - {x_{i - 1}},\;{x_{i - 1}} \le {\xi _i} \le {x_i}.\)

Свойства определенного интеграла

Ниже предполагается, что \(f(x) \ и\ g(x)\) – непрерывные функции на замкнутом интервале \([a;b]\).

1. \(\int\limits_a^b {1dx} = b - a\)
2. \(\int\limits_a^b {kf\left( x \right)dx} = k \int\limits_a^b {f\left( x \right)dx} ,\;\) где \(k\) – константа;
3. \({\int\limits_a^b {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} } = {\int\limits_a^b {f\left( x \right)dx} + \int\limits_a^b {g\left( x \right)dx} }\)
4. \({\int\limits_a^b {f\left( x \right)dx} } = {\int\limits_a^c {f\left( x \right)dx} + \int\limits_c^b {f\left( x \right)dx} ,\;}\) где \(a < c < b;\)
5. Если \(0 \le f\left( x \right) \le g\left( x \right)\) для всех \(x \in \left[ {a;b} \right],\) то \(0 \le \int\limits_a^b {f\left( x \right)dx} \le \int\limits_a^b {g\left( x \right)dx} \).
6. \(\int\limits_a^a {f\left( x \right)dx} = 0\)
7. \(\int\limits_a^b {f\left( x \right)dx} = - \int\limits_b^a {f\left( x \right)dx}\)
8. Пусть точка \(c\) принадлежит отрезку \([a;b]\). Тогда определенный интеграл от функции \(f(x)\) на отрезке \([a;b]\) равен сумме интегралов на частичных промежутках \([a;c] \ и \ [c;b]\): \(\large\int\limits_a^b\normalsize {f\left( x \right)dx} = \large\int\limits_a^c\normalsize {f\left( x \right)dx} + \large\int\limits_c^b\normalsize {f\left( x \right)dx}\)

Пусть функция \(f(x)\) непрерывна на замкнутом интервале \([a;b]\). Если \(F(x)\) – первообразная функции \(f(x) \ на \ [a;b]\), то \({\int\limits_a^b {f\left( x \right)dx} } = {\left. {F\left( x \right)} \right|_a^b } = {F\left( b \right) - F\left( a \right).}\)

Интегрирование по частям для определенного интеграла имеет вид:

\(\int\limits_a^b {udv} = \left. {uv} \right|_a^b - \int\limits_a^b {vdu}.\)

Пример. Вычислить интеграл: \(\int\limits_0^{ln 2} {x{e^{ - x}}dx}\).

Решение: Запишем интеграл в виде \({I = \int\limits_0^{ln 2} {x{e^{ - x}}dx} } = { - \int\limits_0^{ln 2} {xd\left( {{e^{ - x}}} \right)} }\).

Используем интегрирование по частям. В нашем случае пусть будет \({u = x,dv = d\left( {{e^{ - x}}} \right)}\;\; {\Rightarrow du = 1,v = {e^{ - x}}}\).

Следовательно, интеграл равен:

\({I = - \int\limits_0^{ln 2} {xd\left( {{e^{ - x}}} \right)} } = { - \left[ {\left. {\left( {x{e^{ - x}}} \right)} \right|_0^{ln 2} - \int\limits_0^{ln 2} {{e^{ - x}}dx} } \right] } = { - \left. {\left( {x{e^{ - x}}} \right)} \right|_0^{ln 2} + \int\limits_0^{ln 2} {{e^{ - x}}dx} }= \\= { - \left. {\left( {x{e^{ - x}}} \right)} \right|_0^{ln 2} - \left. {\left( {{e^{ - x}}} \right)} \right|_0^{ln 2} } = { - \left. {\left[ {{e^{ - x}}\left( {x + 1} \right)} \right]} \right|_0^{ln 2} } = { - {e^{ - \ln 2}}\left( {ln 2 + 1} \right) + {e^0} \cdot 1 }= \\= { - \frac{{ln 2}}{2} - \frac{{ln e}}{2} + ln e } = {\frac{{ln e}}{2} - \frac{{ln 2}}{2} } = {\frac{1}{2}\left( {ln e - ln 2} \right) } = {\frac{1}{2}ln \frac{e}{2}.}\)