Угловой коэффициент касательной и ее уравнение

Производная функции в данной точке равна тангенсу угла наклона касательной к графику функции в этой точке, или угловому коэффициенту этой касательной: \(f'(x_0)=tg\varphi=k\).

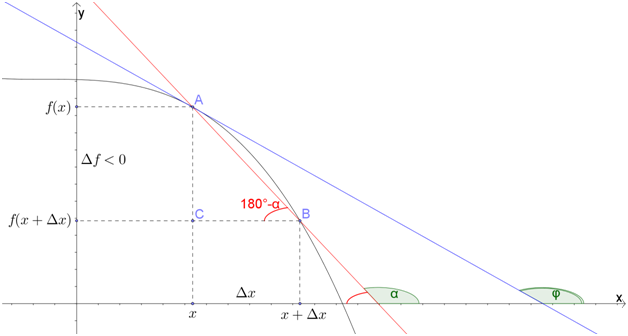
Это и есть геометрический смысл производной.

Касательная прямая – прямая, проходящая через точку кривой и совпадающая с ней в этой точке с точностью до первого порядка.

Прямая, проходящая через точку касания перпендикулярно касательной, называется нормалью к кривой.

Уравнение касательной к графику функции \(y = f(x)\) в точке \(x_0\):  \(y - y_0 = f'(x_0)(x - x_0)\), или \(y = f'(x_0)(x - x_0) + f(x_0)\).

Из геометрии известно, что произведение угловых коэффициентов перпендикулярных прямых равно −1. Поэтому, зная уравнение касательной, можно сразу записать уравнение нормали в виде: \(y - {y_0} = - \frac{1}{{f'\left( {{x_0}} \right)}}\left( {x - {x_0}} \right)\).

Алгоритм решения уравнения касательной к графику функции \(y = f(x)\):

1. Вычислить \(f(x_0)\).
2. Вычислить производные \(f ′(x)\ и\  f ′(x_0)\).
3. Внести найденные числа \(x_0,  f(x_0),  f ′(x_0) \) в уравнение касательной и решить его.

Пример. Найдите уравнение касательной к графику функции \(f(x) = x^3 – 2x^2 + 1\) в точке с абсциссой 2.

Решение:

1) Точка касания \(x_0=2\). Вычислим \(f(x_0)\): \(f(x_0) = f(2) = 2^3 – 2 \cdot 2^2 + 1 = 8 - 8 + 1 = 1\).

2) Находим \(f ′(x)\). Для этого применяем формулы дифференцирования: \(f ′(x) = 3x^2 – 2 \cdot 2x = 3x^2 – 4x\).

Теперь, используя полученное значение \(f ′(x)\), вычислим \(f ′(x_0)\): \(f ′(x_0) = f ′(2) = 3 \cdot2^2 – 4 \cdot 2 = 12 – 8 = 4\).

3) Итак, у нас есть все необходимые данные: \(x_0 = 2, f(x_0) = 1, f ′(x_0) = 4\). Подставляем эти числа в уравнение касательной и находим окончательное решение:

\(y= f(x_0) + f ′(x_0) (x – x_0) = 1 + 4 \cdot(x – 2) = 1 + 4x – 8 = –7 + 4x = 4x – 7\).

Ответ: \(y = 4x– 7\).