Применение производной

Физический смысл производной

Пусть задан путь \(s=f(t)\) движения материальной точки. Скорость данной материальной точки в момент времени \(t\) есть производная от пути \(s\) по времени \(t\): \(v(t)=s'(t)\). А ускорение: \(a(t)=v'(t)=s''(t)\).

Монотонность функции

Функция \(y=f(x)\) называется

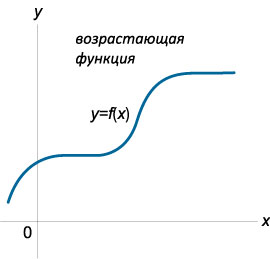
• возрастающей (неубывающей) на интервале (a; b), если \({\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \le f\left( {{x_2}} \right);}\)
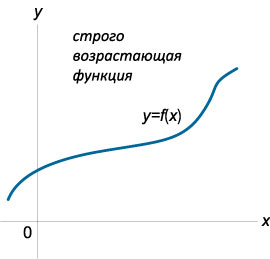
• строго возрастающей на интервале (a; b), если \({\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \lt f\left( {{x_2}} \right);}\)
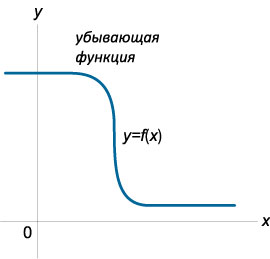
• убывающей (невозрастающей) на интервале (a; b), если \({\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \ge f\left( {{x_2}} \right);}\)
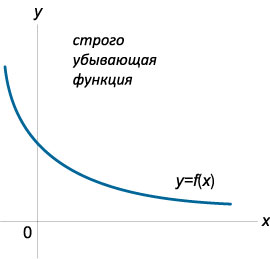
• строго убывающей на интервале (a; b), если \({\forall\;{x_1},{x_2} \in \left( {a,b} \right):\;} {{x_1} < {x_2} \Rightarrow f\left( {{x_1}} \right) \gt f\left( {{x_2}} \right).}\)

Если производная функции \(f'(x)>0\) на некотором промежутке \(X\), то функция \(y=f(x)\) возрастает на этом промежутке; если же \(f'(x)<0\) на промежутке \(X\), то функция \(y=f(x)\) убывает на этом промежутке.

Локальные экстремумы функции

Точка \(x_0\) называется точкой локального максимума функции \(f(x)\), если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство: \(f(x)\le f(x_0)\).

Точка \(x_0\) называется точкой локального минимума функции \(f(x)\), если существует такая окрестность этой точки, что для всех из этой окрестности \(f(x)\ge f(x_0)\).

Локальные максимум и минимум функции называются локальными экстремумами.

Необходимое условие экстремума

Если функция \(y=f(x)\) имеет экстремум в точке \(x_0\), то ее производная \(f'(x_0)\) либо равна нулю, либо не существует.

Точки, в которых производная равна нулю, \(f'(x)=0\), называются стационарными точками функции.

Точки, в которых выполняется необходимое условие экстремума для непрерывной функции, называются критическими точками этой функции. То есть критические точки – это либо стационарные точки (решения уравнения \(f'(x)=0\)), либо это точки, в которых производная \(f'(x)\) не существует.

Первое достаточное условие экстремума

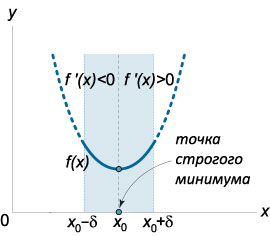
• Если производная \(f′(x)\) меняет знак с минуса на плюс при переходе через точку \(x_0\) (слева направо), то точка \(x_0\) является точкой строгого минимума. Другими словами, в этом случае существует число \(δ>0\), такое, что \(\forall \;x \in \left( {{x_0} - \delta ,{x_0}} \right) \Rightarrow f'\left( x \right) < 0, \\\forall \;x \in \left( {{x_0}, {x_0} + \delta} \right) \Rightarrow f'\left( x \right) > 0.\)
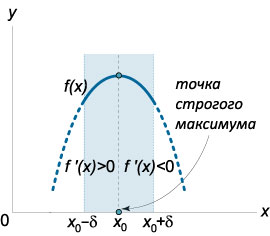
• Если производная \(f′(x)\) меняет знак с плюса на минус при переходе через точку \(x_0\) (слева направо), то точка \(x_0\) является точкой строгого максимума. Другими словами, в этом случае существует число \(δ>0\), такое, что \(\forall \;x \in \left( {{x_0} - \delta ,{x_0}} \right) \Rightarrow f'\left( x \right) > 0, \\\forall \;x \in \left( {{x_0}, {x_0} + \delta} \right) \Rightarrow f'\left( x \right) < 0.\)

Второе достаточное условие экстремума

Пусть в точке \(x_0\) первая производная равна нулю: \(f'(x_0)=0\), т. е. точка \(x_0\) является стационарной точкой функции \(f(x)\). Пусть также в этой точке существует вторая производная \(f''(x_0)\). Тогда:

• если \(f''(x_0)>0, \ то \ x_0\) является точкой строгого минимума функции \(f(x)\);
• если \(f''(x_0)<0, \ то \ x_0\) является точкой строгого максимума функции \(f(x)\).

Выпуклость функции

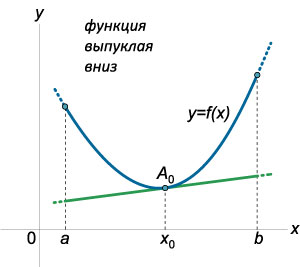
Функция \(f(x)\) является выпуклой вниз на отрезке \([a;b]\) тогда и только тогда, когда ее график лежит не ниже касательной, проведенной к нему в любой точке \(x_0\) отрезка \([a;b]\).

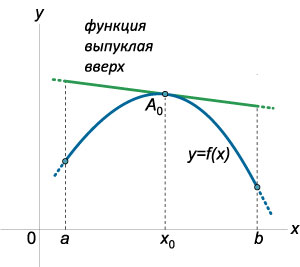
Соответственно, функция \(f(x)\) является выпуклой вверх на отрезке \([a;b]\) тогда и только тогда, когда ее график лежит не выше касательной, проведенной к нему в любой точке \(x_0\) отрезка \( [a;b] \).

Достаточные условия выпуклости

Пусть для функции \(f(x)\) первая производная \(f'(x)\) существует на отрезке \([a;b]\), а вторая производная \(f''(x)\) − на интервале \((a;b)\). Тогда справедливы следующие достаточные признаки выпуклости:

• если \(f''(x)≥0\) при всех \(x\in(a;b)\), то функция \(f(x)\) выпуклая вниз на отрезке \([a;b]\);
• если \(f''(x)\le0\) при всех \(x\in(a;b)\), то функция \(f(x)\) выпуклая вверх на отрезке \([a;b]\);

В тех случаях, когда вторая производная строго больше (меньше) нуля, говорят, соответственно, о строгой выпуклости вниз (или вверх).

Точка перегиба

Если первая производная \(f'(x_0)\) существует в точке \(x_0\), а вторая производная \(f''(x_0)\) меняет знак при переходе через \(x=x_0\), то точка \((x_0,f(x_0))\) называется точкой перегиба графика функции \( f(x)\). Если вторая производная \(f''(x_0)\) существует в точке перегиба, то она равна нулю: \(f''(x_0)=0\).