Векторы и координаты

Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси.

• Единичный вектор, направленный вдоль оси x, обозначается как $\vec i$.
• Единичный вектор, направленный вдоль оси y, обозначается как $\vec j$.

Векторы $\vec i \ и \ \vec j$ ортогональны.

Любой вектор $\vec a$ можно разложить по координатным векторам: $\vec a = a_x \cdot \vec i+a_y \cdot \vec j$.

Чтобы найти координаты вектора $\vec{ AB}$, если заданы координаты его начала и конца, необходимо от координат конца отнять соответствующие координаты начала. В случае, если точки заданы на плоскости и имеют соответственно координаты $A(x_A;y_A) \ и \ B(x_B;y_B)$, то координаты вектора $\vec{AB}$ вычисляются по формуле: $\vec{AB}=(x_B-x_A; y_B-y_A)$.

Пример 1. Даны точки $A(5;1) \ и \ B(4;-3)$. Найти координаты вектора $\vec{AB}$.

Решение: Точки заданы на плоскости, поэтому координаты вектора $\vec{AB}$ вычислим по формуле:

$\vec{AB}=(x_B-x_A; y_B-y_A)$. Подставляя координаты заданных точек, получим: $\vec{AB}=(4-5; -3-1)=(-1;-4)$.

Чтобы найти сумму векторов $\vec a+\vec b$, которые заданы координатами $\vec a=(a_x;a_y) \ и \ \vec b=(b_x;b_y)$, необходимо сложить соответствующие координаты этих векторов, то есть $\vec a+\vec b=(a_x+b_x;a_y+b_y)$.

Чтобы найти разность векторов $\vec a-\vec b$, заданных на плоскости координатами $\vec a=(a_x;a_y) \ и \ \vec b=(b_x;b_y)$, необходимо вычесть из координат первого вектора соответствующие координаты второго, то есть $\vec a-\vec b=(a_x-b_x;a_y-b_y)$.

Чтобы найти длину вектора, заданного своими координатами, нужно извлечь корень квадратный из суммы квадратов его координат. Если вектор задан на плоскости и имеет координаты $\vec a=(a_x;a_y)$, его длина вычисляется по формуле: $|\vec a|=\sqrt{a^2_x+a^2_y}$.

Для того чтобы найти скалярное произведение двух векторов, заданных своими координатами, необходимо вычислить сумму произведений соответствующих координат этих векторов. Для случая, если векторы заданны на плоскости координатами $\vec a=(a_x;a_y) \ и \ \vec b=(b_x;b_y)$, имеет место формула: $(\vec a, \vec b)=a_x\cdot b_x+a_y \cdot b_y$.

Чтобы найти угол $\alpha$ между векторами, нужно вначале найти косинус угла, а затем от него найти арккосинус, то есть: $\alpha=arccos(cos\alpha)$. Косинус угла между векторами равен скалярному произведению этих векторов, деленному на произведение их длин. В случае, если векторы заданы на плоскости и имеют координаты $\vec a=(a_x;a_y),\vec b=(b_x;b_y)$, то косинус между ними вычисляется по формуле: $cos\alpha=\frac{(\vec a,\vec b)}{|\vec a| \cdot |\vec b|}=\frac{a_x\cdot b_x+a_y \cdot b_y}{\sqrt{a^2_x+a^2_y}\cdot \sqrt{b^2_x+b^2_y}}$.

Для того чтобы вектор $\vec a=(a_x;a_y)$ был коллинеарным вектору $\vec b=(b_x;b_y)$, необходимо, чтобы их соответствующие координаты были пропорциональны, то есть их координаты удовлетворяли условию $\frac{a_x}{b_x}=\frac{a_y}{b_y}$.

Пример 2. Даны два вектора $\vec a=(2;-3) \ и \ \vec b=(-1;m)$. При каком значении 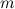эти векторы будут коллинеарными?

Решение: Для того чтобы векторы $\vec a \  и \ \vec b$ были коллинеарными, необходимо, чтобы их координаты были пропорциональными, то есть удовлетворяли условию: $\frac{a_x}{b_x}=\frac{a_y}{b_y}$.

Подставим координаты заданных векторов в это равенство и найдем значение $m$: $\frac2{-1}=\frac{-3}{m}$. По пропорции, имеем: $2\cdot m=(-1)\cdot (-3) \Rightarrow 2m=3 \Rightarrow m=\frac32=1,5$.

Ответ: Векторы $\vec a \  и \ \vec b$ будут коллинеарными при $m=1,5$.

Для того чтобы вектор $\vec a$ был перпендикулярен вектору $\vec b$, необходимо, чтобы их скалярное произведение было равно нулю, то есть $(\vec a, \vec b)=0$. В случае, если векторы заданы на плоскости своими координатами $\vec a=(a_x;a_y) \ и \ \vec b=(b_x;b_y)$, то условие их перпендикулярности примет вид: $(\vec a, \vec b)=a_x\cdot b_x+a_y\cdot b_y=0$.