Действия над векторами и их свойства

Сложение векторов

Суммой двух векторов \(\mathbf{\vec{u}}\) и \(\mathbf{\vec{v}}\) называется третий вектор \(\mathbf{\vec{w}}\), проведенный из начала \(\mathbf{\vec{u}}\) к концу \(\mathbf{\vec{v}}\), если начало вектора \(\mathbf{\vec{v}}\) совпадает с концом вектора \(\mathbf{\vec{u}}\). Сложение векторов выполняется по правилу треугольника или по правилу параллелограмма.

\(\mathbf{\vec{w}} = \mathbf{\vec{u}} + \mathbf{\vec{v}}\)

Суммой нескольких векторов \(\mathbf{\vec{u_1}},\mathbf{\vec{u_2}}, \mathbf{\vec{u_3}}\)… называется вектор \(\mathbf{\vec{w}}\), получающийся в результате последовательного сложения данных векторов. Такая операция выполняется по правилу многоугольника.

\(\mathbf{\vec{w}} = \mathbf{\vec{u_1}} + \mathbf{\vec{u_2} }+ \mathbf{\vec{u_3}} + \ldots + \mathbf{\vec{u_n}}\)

Разность векторов

Разностью двух векторов \(\mathbf{\vec{u}}\) и \(\mathbf{\vec{v}}\) называется вектор \(\mathbf{\vec{w}}\) при условии: \(\mathbf{\vec{w}}=\mathbf{\vec{u}}-\mathbf{\vec{v}}\), если \(\mathbf{\vec{w}}+\mathbf{\vec{v}}=\mathbf{\vec{u}}\).

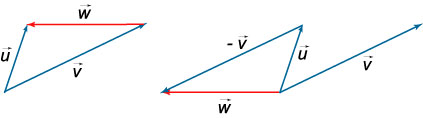
Разность векторов \(\mathbf{\vec{u}}\) и \(\mathbf{\vec{v}}\) равна сумме вектора \(\mathbf{\vec{u}}\) и противоположного вектора \(-\mathbf{\vec{v}}\):  \(\mathbf{\vec{u}} - \mathbf{\vec{v}} = \mathbf{\vec{u}} + \left( -\mathbf{\vec{v}} \right)\).

Умножение вектора на число

Произведением вектора \(\mathbf{\vec{u}} \ne \mathbf{0}\) на число \(\lambda \ne 0\) называется вектор \(\mathbf{\vec{w}}\), модуль которого равен \(\left| \lambda \right| \cdot \left| \mathbf{\vec{u}} \right|\), направление которого совпадает с вектором \(\mathbf{\vec{u}}\) при \(\lambda > 0\) и противоположно ему при \(\lambda < 0\).

\(\mathbf{\vec{w}} = \lambda \mathbf{\vec{u}},\;\;\left| \mathbf{\vec{w}} \right| = \left| \lambda \right| \cdot \left| \mathbf{\vec{u}} \right|\)

Свойства линейных операций над векторами

Сложение векторов и умножение вектора на число называются линейными операциями над векторами. Для любых векторов \(\vec a\), \(\vec b\), \(\vec c\) и любых действительных чисел \(\alpha, \beta\) справедливы равенства:

\(1.\ \vec a + \vec b = \vec b + \vec a;\\ 2.\ (\vec a + \vec b) + \vec c = \vec a + (\vec b + \vec c);\\ 3.\ \vec a + \vec o = \vec a;\\ 4.\ \vec a + (- \vec a) = \vec o; \\ 5.\ (\alpha \beta) \cdot \vec a = \alpha (\beta \cdot \vec a);\\ 6.\ (\alpha + \beta) \cdot \vec a = \alpha \cdot \vec a + \beta \cdot \vec a;\\ 7.\ \alpha \cdot (\vec a + \vec b) = \alpha \cdot \vec a + \alpha \cdot \vec b;\\ 8.\ 1 \cdot \vec a = \vec a.\)

Свойства 1, 2 выражают коммутативность и ассоциативность операции сложения векторов; свойство 5 – ассоциативность операции умножения на число; свойства 6, 7 – законы дистрибутивности; свойство 8 называется унитарностью.