Арифметическая прогрессия

Прогрессия – это последовательность чисел, получаемых по некоторому правилу. Числа составляющие последовательность, называются ее членами.

Арифметической прогрессией называется числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

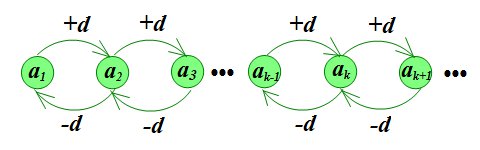
Число \(d=a_k-a_{k-1}\) называется разностью арифметической прогрессии. Разность арифметической прогрессии может быть положительной, отрицательной, или равной нулю.

Если \(d>0\), то каждый член арифметической прогрессии больше предыдущего, и прогрессия является возрастающей.

Например, 2; 5; 8; 11;... \(d=3\).

Если \(d<0\), то каждый член арифметической прогрессии меньше предыдущего, и прогрессия является убывающей.

Например, 2; –1; –4; -7;... \(d=-3\).

Если \(d=0\), то все члены прогрессии равны одному и тому же числу, и прогрессия является стационарной.

Например, 2; 2; 2; 2;...

Зная первый член и разность арифметической прогрессии, можно найти любой ее член: \(a_n = a_1+ d( n-1)\).

Свойство арифметической прогрессии

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних: \(a_k=\frac{a_{k-1}+a_{k+1}}2\).

Пример 1. Задана арифметическая прогрессия, где пятый и десятый члены равны соответственно 38 и 23. Найдите пятнадцатый член прогрессии.

Решение: Так как \(a_n = a_1+ d( n-1)\), то

\(\begin{cases} a_5=38\\ a_{10}=23 \\ \end{cases} \Rightarrow \begin{cases} a_5=a_1+4d=38\\ a_{10}=a_1+9d=23 \\ \end{cases} \Rightarrow -5d=15; \ d=-3\)

\(a_1=38-4\cdot(-3)=50 \\a_{15}=a_1+14d=50+14\cdot (-3)=8\)

Ответ: 8.

Сумму любого количества первых членов арифметической прогрессии можно найти с помощью формулы: \(S_n=\frac{a_1+a_n}2n\).

Если заданы первый член и разность арифметической прогрессии, то удобно пользоваться другой формулой: \(S_n=\frac{2a_1+d(n-1)}2n\).

Пример 2. Четвертый член арифметической прогрессии равен 9, а восьмой равен 7. Найти сумму пяти членов прогрессии.

Решение: \(\begin{cases} a_4=9\\ a_{8}=7 \\ \end{cases} \Rightarrow \begin{cases} a_4=a_1+3d=9\\ a_{8}=a_1+7d=7 \\ \end{cases} \Rightarrow 4d=-2; \ d=-\frac12\)

Подставим \(d=-\frac12\) в первое уравнение системы: \(a_1+3\cdot(-\frac12)=9 \Rightarrow a_1=10,5\).

Теперь найдем \(S_5\):

\(S_5=\frac{2a_1+d(5-1)}2\cdot 5=\frac{2\cdot 10,5+(-\frac12)\cdot 4}2 \cdot5=47,5\)

Ответ: 47,5.