Основное тригонометрическое тождество и его следствия

$\cos \alpha = \frac{AC}{AB} \ \ \ (1); \ \sin \alpha = \frac{BC}{AB} \ \ \ (2); \ {\rm tg}\, \alpha = \frac{BC}{AC} \ \ \ (3);$

Используя равенства (1), (2) и (3), имеем: $\sin \alpha \cdot \frac{1}{\cos \alpha} = \frac{BC}{AB} \cdot \frac{AB}{AC} = \frac{BC}{AC} = {\rm tg}\, \alpha$. Итак, ${\rm tg}\, \alpha = \frac{\sin \alpha}{\cos \alpha}$.

Соответственно, ${\rm ctg}\, \alpha = \frac{\cos \alpha}{\sin \alpha}$.

Получаем: ${\rm tg}\alpha = \frac{1}{ {\rm ctg}\, \alpha } ; \ \ \ {\rm ctg}\, \alpha = \frac{1}{ {\rm tg}\, \alpha }$.

Далее, используя определения синуса, косинуса и теорему Пифагора, находим:

$\sin^2 \alpha + \cos^2 \alpha = \frac{BC^2}{AB^2} + \frac{BC^2}{AB^2} = \frac{BC^2 + AC^2}{AB^2} = \frac{AB^2}{AB^2} = 1 \ \ (4)$

Итак, имеем тождество: $\sin^2 \alpha + \cos^2 \alpha = 1$.

Используя тождество (4), получаем: $1 + {\rm tg^2}\, \alpha = 1 + \frac{\sin^2 \alpha}{\cos^2 \alpha} = \frac{\cos^2 \alpha + \sin^2 \alpha}{\cos^2 \alpha} = \frac{1}{\cos^2 \alpha}$.

Таким образом: $1 + {\rm tg^2}\, \alpha = 1 + \frac{1}{{\rm ctg^2}\, \alpha} = \frac{1}{cos^2 \alpha}$.

Аналогично выводится тождество: $1 + \frac{1}{{\rm tg^2}\, \alpha} = 1 + {\rm ctg^2}\, \alpha = \frac{1}{sin^2 \alpha}$.

Пример 1. Вычислить значение $\cos \alpha$ и ${\rm tg}\, \alpha$, если $\sin \alpha = \frac{1}{2}$.

Решение:

Так как $\sin^2 \alpha + \cos^2 \alpha = 1$, то

$\cos \alpha = \sqrt{1 - \sin ^2 \alpha} = \sqrt{1 - \left ( \frac{1}{2} \right ) ^2} = \frac{ \sqrt{3} }{2} \\ {\rm tg}\, \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{1 \cdot2}{2 \cdot \sqrt{3} } = \frac {1}{\sqrt{3}} = \frac{\sqrt{3}}{3}.$

Теорема. Для любого острого угла $\alpha$:

$\sin (90° - \alpha) = \cos \alpha \\ \cos (90° - \alpha) = \sin \alpha$

Пример 2. Найти значения sin 45°, cos 45° и tg 45°.

Решение: Рассмотрим равнобедренный прямоугольный треугольник.

В нем каждый острый угол равен 45°. Пусть его катеты равны а. По теореме Пифагора, его гипотенуза равна $a\sqrt{2}$.

Теперь, по определению, имеем:

$\sin 45° = \frac{a}{a \sqrt{2} } = \frac{1}{ \sqrt{2} } = \frac{ \sqrt{2} }{2} \\ \cos 45° = \frac{a}{a \sqrt{2} } = \frac{1}{ \sqrt{2} } = \frac{ \sqrt{2} }{2} \\ {\rm tg}\, 45° = \frac{a}{a} = 1$

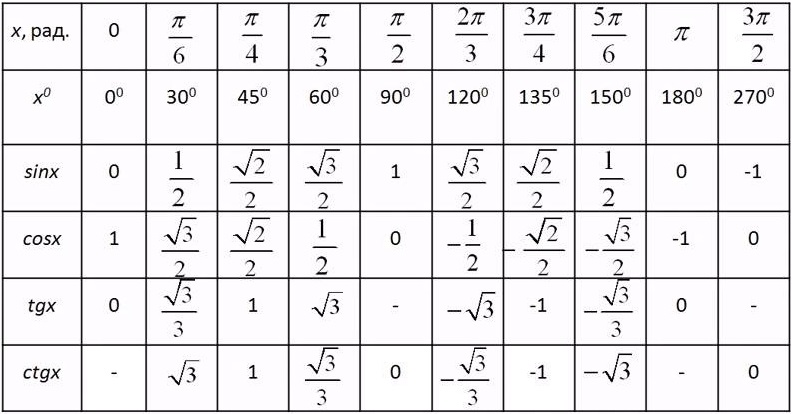
Значение тригонометрических функций некоторых углов