+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Взаимное расположение прямой и окружности
Предыдущий конспект Следующий конспект
Конспект

Существует 3 случая взаимного расположения прямой и окружности в зависимости от соотношения между радиусом r окружности и расстоянием d прямой от центра окружности.

1. d < r. Если расстояние от центра окружности до прямой меньше радиуса окружности, то окружность и прямая имеют две общие точки.

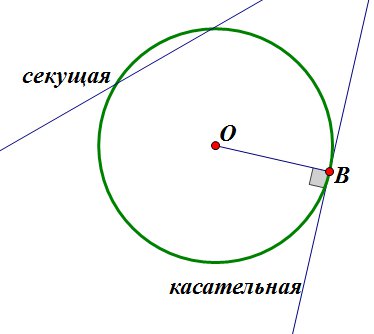
2. d = r. Если расстояние от центра окружности до прямой равно радиусу окружности, то прямая и окружность имеют единственную общую точку.

3. d > r. Если расстояние от центра окружности до прямой больше радиуса окружности, то прямая и окружность не имеют общих точек.

Прямая, имеющая с окружностью ровно одну общую точку, называется касательной к окружности, а их общая точка называется точкой касания прямой и окружности. Прямая, имеющая с окружностью две общие точки, называется секущей.

Теоремы о касательных и секущих

  1. Касательная к окружности перпендикулярна радиусу, проведенному к точке касания.

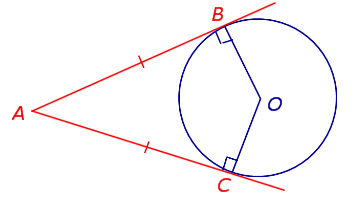
  1. Если из данной точки проведены к окружности две касательные, то отрезки касательных равны между собой и центр окружности лежит на биссектрисе угла с вершиной в этой точке: \(AB=AC\).

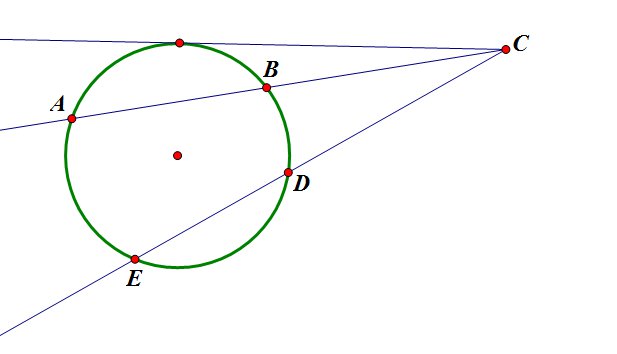
Теоремы о длинах хорд касательных и секущих

  1. Если из данной точки проведены к окружности касательная и секущая, то квадрат длины отрезка касательной равен произведению всего отрезка секущей на его внешнюю часть: \(AC^2=CD\cdot BC\).

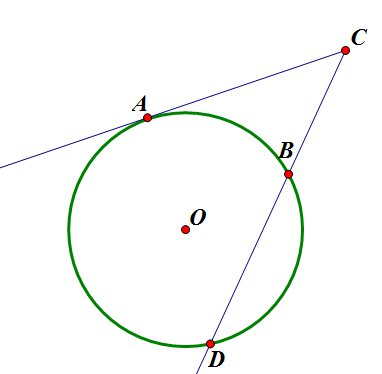
  1. Произведение всего отрезка одной секущей на его внешнюю часть равно произведению всего отрезка другой секущей на его внешнюю часть: \(AC\cdot BC=EC\cdot DC\).



Сообщить об ошибке