+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Центральные углы. Градусная мера дуги
Предыдущий конспект Следующий конспект
Конспект

Центральным углом называют угол, вершина которого совпадает с центром окружности, а стороны являются радиусами.

Вписанный угол – угол, вершина которого лежит на окружности, а стороны являются ее хордами.

Вписанные и центральные углы

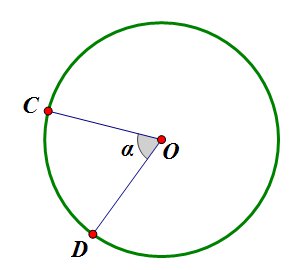
Градусная величина дуги окружности измеряется величиной центрального угла, который на нее опирается.

Теоремы о вписанных и центральных углах

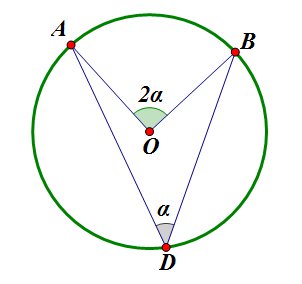
  1. Вписанный угол измеряется половиной дуги, на которую он опирается: \(\angle AOB=2\angle ADB\).
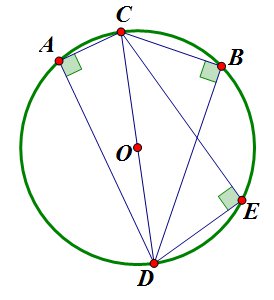
  2. Вписанный угол, опирающийся на диаметр, является прямым.
  3. Вписанные углы, опирающиеся на одну дугу, равны: \(∠ADB=∠AEB=∠AFB\).
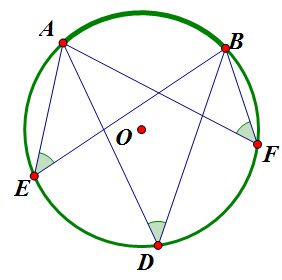
  4. Вписанные углы, опирающиеся на одну хорду равны, или их сумма равна 180°: \(∠ADB+∠AKB=180 ^{\circ}; \ \ \ \ ∠ADB=∠AEB=∠AFB\).
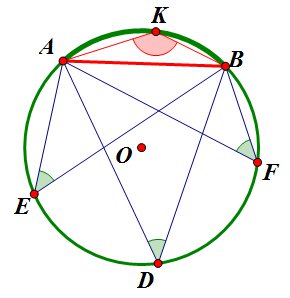
  5. Вписанный угол является прямым углом тогда и только тогда, когда он опирается на диаметр.

Теоремы об углах, образованных хордами, касательными и секущими

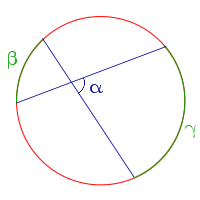
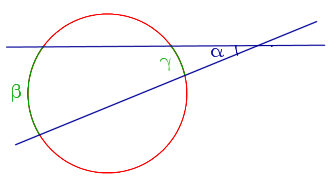
  1. Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключенных между его сторонами: \(\alpha=\frac{\beta+\gamma}{2}\). Теоремы об углах образованных хордами касательными и секущими
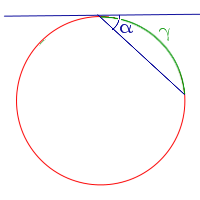
  2. Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключенных между его сторонами: \(\alpha=\frac{\beta-\gamma}{2}\). Теоремы об углах образованных хордами касательными и секущими
  3. Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключенной между его сторонами: \(\alpha=\frac{\gamma}{2}\). Теоремы об углах образованных хордами касательными и секущими

 



Вопросы

  1. Най­ди­те впи­сан­ный угол, опи­ра­ю­щий­ся на дугу, ко­то­рая со­став­ля­ет 20% окруж­но­сти.

  2. В окруж­но­сти с цен­тром O от­рез­ки AC и BD – диа­мет­ры. Впи­сан­ный угол ACB равен 38\(^\circ\). Най­ди­те цен­траль­ный угол AOD.

  3. Най­ди­те цен­траль­ный угол AOB, если он на 15\(^\circ\) боль­ше впи­сан­но­го угла ACB, опи­ра­ю­ще­го­ся на ту же дугу.

  4. Окружность поделена тремя точками в отношении 2:5:11. Определите углы полученного треугольника.

  5. Окружность поделена тремя точками в отношении 3:5:10. Определите углы полученного треугольника.

  6. Окружность поделена тремя точками в отношении 3:5:4. Найдите углы полученного треугольника.

Сообщить об ошибке