+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Вписанные и описанные окружности
Предыдущий конспект Следующий конспект
Конспект

Окружность называется вписанной в многоугольник, если она касается его сторон. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Не во всякий многоугольник можно вписать окружность.

Площадь многоугольника, в который вписана окружность, можно найти по формуле: \(S=pr\), здесь \(p\) – полупериметр многоугольника, \(r\) – радиус вписанной окружности.

Если в выпуклый четырехугольник вписана окружность, то суммы длин противоположных сторон равны. Обратно: если в выпуклом четырехугольнике суммы длин противоположных сторон равны, то в четырехугольник можно вписать окружность:

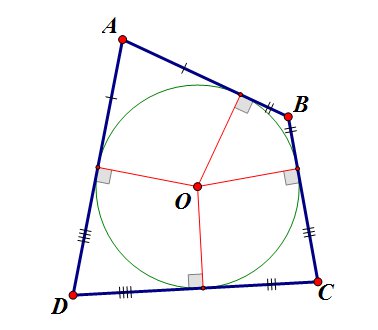
\(AB+DC=AD+BC\).

В любой треугольник можно вписать окружность, притом только одну.

Центр вписанной окружности лежит в точке пересечения биссектрис внутренних углов треугольника.

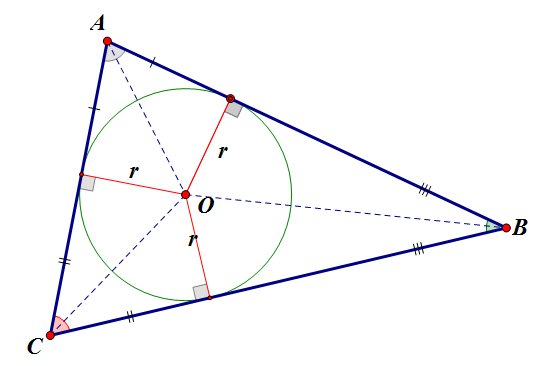
Радиус вписанной окружности равен \(r=\frac{S}{p}\), здесь \(p=\frac{a+b+c}{2}\).

Окружность называется описанной около многоугольника, если она проходит через все вершины многоугольника. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров сторон многоугольника.

Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180°.

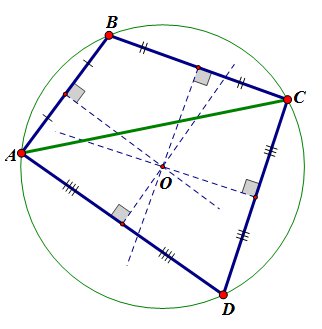
\(∠A+∠C=∠B+∠D=180^{\circ}\).

Около любого треугольника можно описать окружность, притом только одну. Ее центр лежит в точке пересечения серединных перпендикуляров сторон треугольника.

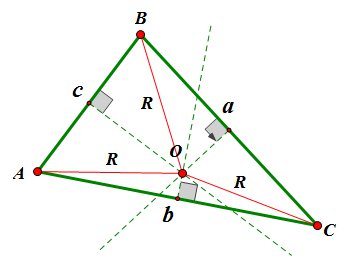
Радиус описанной окружности вычисляется по формулам:

\(\begin{aligned} &R=\frac{a}{2sinA}=\frac{b}{2sinB}=\frac{c}{2sinC}; \\[6pt] &R=\frac{abc}{4S}. \end{aligned}\)

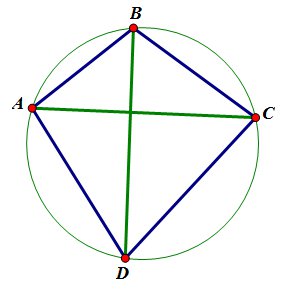
Теорема Птолемея

Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его противоположных сторон: \(AC\cdot BD=AB\cdot CD+BC\cdot AD\).



Вопросы

  1. В прямоугольном треугольнике точка касания вписанной окружности делит гипотенузу на отрезки длиной 5 и 12 см. Найдите катеты треугольника.

  2. Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 13 и 5, считая от противолежащей основанию вершины. Найдите периметр треугольника.

  3. Бо­ко­вая сто­ро­на рав­но­бед­рен­ной тра­пе­ции равна ее мень­ше­му ос­но­ва­нию, угол при ос­но­ва­нии равен 60°, боль­шее ос­но­ва­ние равно 12 см. Най­ди­те ра­ди­ус опи­сан­ной окруж­но­сти этой тра­пе­ции.

  4. Окруж­ность, впи­сан­ная в рав­но­бед­рен­ный тре­уголь­ник, делит в точке ка­са­ния одну из бо­ко­вых сто­рон на два от­рез­ка, длины ко­то­рых равны 5 и 3, счи­тая от про­ти­во­ле­жа­щей ос­но­ва­нию вер­ши­ны. Най­ди­те пе­ри­метр тре­уголь­ни­ка.

Сообщить об ошибке