+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Свойство и признаки равнобедренного треугольника
Предыдущий конспект Следующий конспект
Конспект

Треугольник называется равнобедренным, если у него две стороны равны.

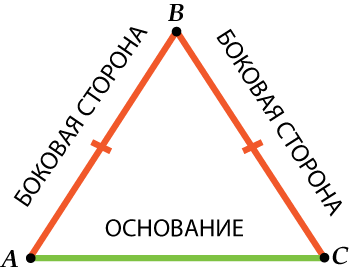
Равнобедренный треугольник (2)

Свойства равнобедренного треугольника

  1. В равнобедренном треугольнике углы при основании равны.
  2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
  3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
  4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
  5. Центры вписанной и описанной окружностей лежат на высоте, биссектрисе и медиане (они совпадают), проведенных к основанию.

Признаки равнобедренного треугольника

  1. Если в треугольнике два угла равны, то он равнобедренный.
  2. Если в треугольнике медиана является высотой, то он равнобедренный.
  3. Если в треугольнике медиана является биссектрисой, то он равнобедренный.
  4. Если в треугольнике высота является биссектрисой, то он равнобедренный.

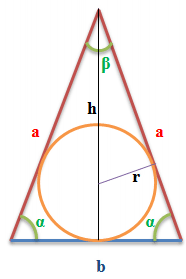
Равнобедренный треугольник с обозначениями сторон и углов, которые применяются в общепринятых формулах

Формулы длины стороны

\(1) \ b=2a\cdot cos\alpha \ \Rightarrow a=\frac{b}{cos\alpha} \\2) \ b=2a\cdot sin(\frac{\beta}2)=a\sqrt{2-2cos\beta} \)

Формулы биссектрисы, медианы и высоты

\(1) \ h=a\cdot sin\alpha \\ 2) \ h=\frac{b}2\cdot tg\alpha \\3)\ h=a\cdot cos(\frac{\beta}{2}) \\4)\ h=\sqrt{a^2-\frac{b^2}{4}}\)

Формулы радиуса вписанной окружности в равнобедренный треугольник

\(1)\ r=\frac{b}2\sqrt{\frac{2a-b}{2a+b}} \\2)\ r=\frac{bh}{b+\sqrt{4h^2+b^2}} \\3)\ r=\frac{b}{2}\cdot tg\frac{\alpha}{2} \\4)\ r=a\cdot cos\alpha\cdot tg\frac{\alpha}{2}\)



Вопросы

  1. Периметр равнобедренного треугольника равен 18 м. Найдите его стороны, если основание больше боковой стороны на 3 м.

Сообщить об ошибке