+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Окружность и ее элементы
Предыдущий конспект Следующий конспект
Конспект

Окружностью называется множество точек, расположенных на одинаковом расстоянии от данной точки, которая называется центром окружности.

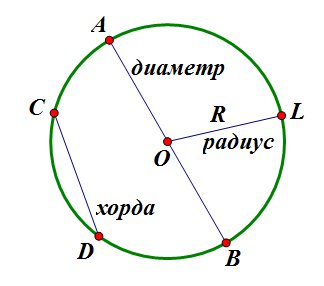
Отрезок, соединяющий центр окружности с любой точкой окружности, называют радиусом. Отрезок, соединяющий любые две точки окружности, называют хордой. Хорда, проходящая через центр окружности, называется диаметром.

Уравнение окружности с радиусом \(R\) и с центром в точке \(O ( x_0; y_0 )\) имеет вид:

\((x-x_0 ) ^2  + ( y-y_0) ^2 = R^ 2\).

Длина окружности: \(C=2\pi R\).

Площадь круга: \(S=\pi R^2\).

Часть окружности, заключенная между двумя ее точками, называется дугой окружности. Две точки окружности определяют две дуги.

Длина дуги окружности: \(l=Ra=\frac{\pi R \alpha}{180^{\circ}}\), \(a\) – радианная мера дуги, \( \alpha\) – градусная мера.

Свойства хорд и дуг окружности

  1. Диаметр, перпендикулярный хорде, делит эту хорду и дуги, которые она стягивает пополам.

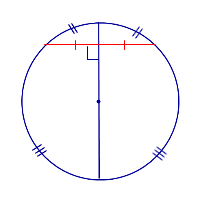
Свойства хорд и дуг окружности

  1. Если хорды равны, то они находятся на одном и том же расстоянии от центра окружности.

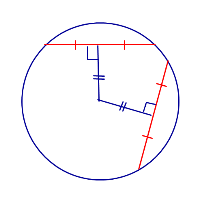
Свойства хорд и дуг окружности

  1. Большая из двух хорд расположена ближе к центру окружности.
  2. У равных дуг равны и хорды.

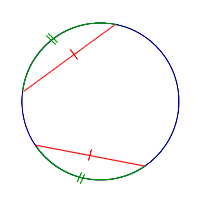
Свойства хорд и дуг окружности

  1. Дуги, заключенные между параллельными хордами, равны.
  2. Произведения длин отрезков, на которые разбита каждая из хорд, равны: \(AE\cdot EB=CE\cdot ED\).

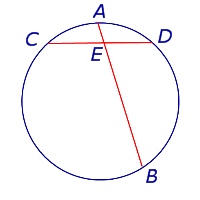
Свойства хорд и дуг окружности​​​​​​​



Вопросы

  1. Часть окружности, ограниченная двумя точками, это

Сообщить об ошибке