Уравнения с параметрами

Уравнение с параметрами – математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров.

Решить уравнение с параметром означает:

1. Найти все системы значений параметров, при которых данное уравнение имеет решение.
2. Найти все решения для каждой найденной системы значений параметров, то есть для неизвестного и параметра должны быть указаны свои области допустимых значений.

Пример 1. Решить уравнение и определить знаки корней: \(ax+2x+3=1-x\).

Решение: \(ax + 2x + x = 1 - 3 \Rightarrow ax + 3x = -2 \Rightarrow (a + 3)x = -2\).

При \(a = – 3\) уравнение \(0·x = – 2\) не имеет решений.

При \(a \ne – 3\) решение \(x=-\frac2{a+3}\).

Решение будет положительным, если: \(-\frac2{a+3}>0 \Rightarrow a+3<0 \Rightarrow a<-3\).

Решение будет отрицательным, если: \(-\frac2{a+3}<0 \Rightarrow a+3>0 \Rightarrow a>-3\).

Ответ: \(при \ a = – 3 \Rightarrow x\in \varnothing ; \\при \ a \ne – 3\Rightarrow x=-\frac2{a+3} ; \\при \ a < – 3\Rightarrow x > 0; \\при \ a > – 3\Rightarrow x < 0.\)

Пример 2. Найдите все значения параметра \(a\), при каждом из которых корень уравнения \(3x(a+4)=6a+35\) в три раза меньше корня уравнения \(2(-x-1)=3(2-x)\).

Решение: Если \(x = 8\) корень уравнения \(2(-x-1)=3(2-x)\), то \(x=\frac83\) корень уравнения \(3x(a+4)=6a+35\) (по условию). Подставим \(x=\frac83\) в уравнение \(3x(a+4)=6a+35\):

\(3\cdot \frac83(a+4)=6a+35 \Rightarrow 8a+32=6a+35 \Rightarrow 2a=3 \Rightarrow a=\frac32\).

Ответ: \(a=\frac32\).

Пример 3. При каких значениях \(a\) корни уравнения \((a-2)x^2-2ax+a+3=0\) положительны?

Решение:

1. Начнем с рассмотрения случая, когда \(a=2\). Тогда уравнение принимает вид \(-4x+5=0\), откуда получаем, что \(x=\frac54\) – положительный корень. Значит, данное значение \(a\) нам подходит. Запомнили.

2. Теперь рассматриваем случай, когда \(a\ne2\). Получается квадратное уравнение. Определим сначала при каких значениях 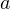данное уравнение имеет корни. Нужно, чтобы его дискриминант был неотрицателен. То есть:\(D=4a^2-4(a-2)(a+3)=-4a+24\ge0 \Leftrightarrow a\le 6\).

Корни, по условию, должны быть положительны, следовательно, имеет место система:

\(\begin{cases} \frac{2a+\sqrt{24-4a}}{2a-4}>0 \\ \frac{2a-\sqrt{24-4a}}{2a-4}>0 \\ a\le6 \end{cases} \Rightarrow \begin{cases} a\in(-\infty;-3)\cup(2;6] \\ a\in(-\infty;2)\cup(2;6]\\ a\in(-\infty;6] \end{cases} \Rightarrow a\in(-\infty;-3)\cup(2;6].\)

3. Объединяем ответы, полученные в предыдущих двух пунктах, и получаем искомый промежуток: \(a\in (-\infty;-3)\cup[2;6]\).

Ответ: \(a\in (-\infty;-3)\cup[2;6]\).