Параллелепипед. Призма

Призмой называется многогранник, составленный из двух равных многоугольников \(A_1A_2...A_n \ и \ B_1B_2...B_n\), лежащих в параллельных плоскостях, и \(n\) параллелограммов\(A_1A_2B_2B_1,...,A_1A_nB_nB_1\).

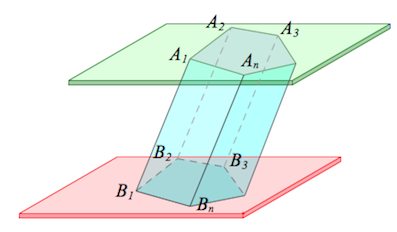
Указанные в определении равные многоугольники – основания призмы.

Боковые грани – все грани, кроме оснований (являются параллелограммами).

Боковые ребра – общие стороны боковых граней (параллельны между собой и равны).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

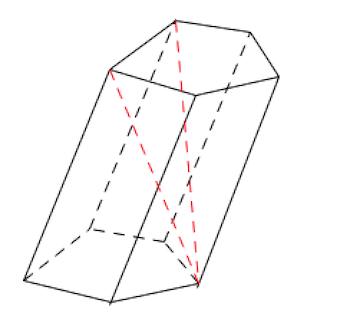
Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

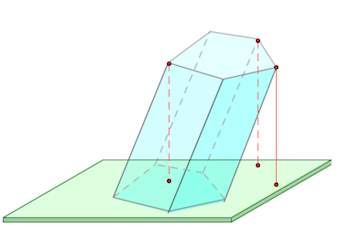
Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение – пересечение призмы и диагональной плоскости.

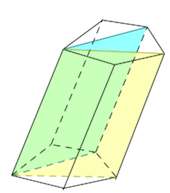
Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

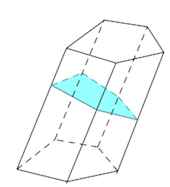
Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

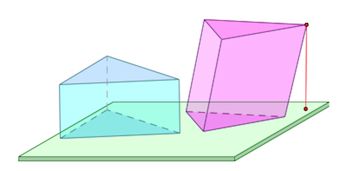
Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т. п.).

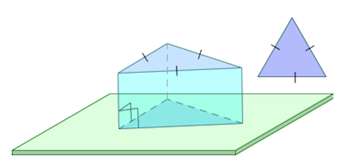
Частным случаем призмы является параллелепипед.

Параллелепипед – это призма, основание которой – параллелограмм. Параллелепипед имеет шесть граней, и все они параллелограммы. Противоположные грани попарно равны и параллельны. Параллелепипед имеет четыре диагонали. Все диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. Основанием параллелепипеда может быть любая грань.

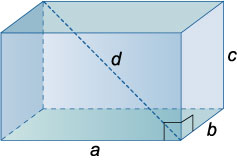
Параллелепипед, четыре боковые грани которого – прямоугольники, называется прямым. Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным. Прямоугольный параллелепипед, все грани которого – квадраты, называется кубом. Все ребра куба равны.

Свойства параллелепипеда:

• Параллелепипед симметричен относительно середины его диагонали.
• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
• Противолежащие грани параллелепипеда параллельны и равны.
• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.