Пирамида. Усеченная пирамида

Пирамида – многогранник, основание которого – многоугольник, а остальные грани – треугольники, имеющие общую вершину.

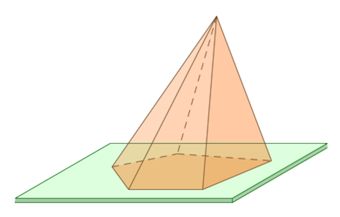
По числу углов основания различают пирамиды треугольные, четырехугольные и т. д.

Вершина пирамиды – точка, соединяющая боковые ребра и не лежащая в плоскости основания.

Основание – многоугольник, которому не принадлежит вершина пирамиды.

Апофема – высота боковой грани правильной пирамиды, проведенная из ее вершины. В правильной пирамиде длина апофемы выражается формулой \(m = \sqrt {{b^2} - \large\frac{{{a^2}}}{4}\normalsize}\).

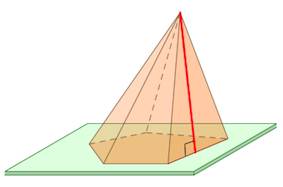
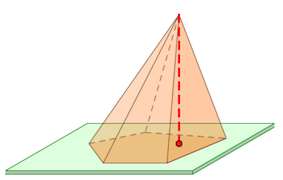
Высота – отрезок перпендикуляра, проведенного через вершину пирамиды к плоскости ее основания (концами этого отрезка являются вершина пирамиды и основание перпендикуляра). В правильной пирамиде высота равна \(h = \large\frac{{\sqrt {4{b^2}{{\sin }^2}\frac{\pi }{n} - {a^2}} }}{{2\sin \frac{\pi }{n}}}\normalsize\), где \(b\) − боковое ребро, \(a\) − сторона основания, \(n\) − число сторон многоугольника в основании.

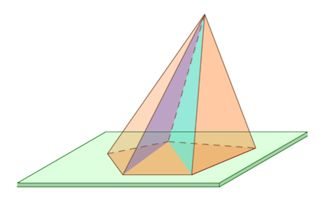
Диагональное сечение пирамиды – сечение пирамиды, проходящее через вершину и диагональ основания.

Некоторые свойства пирамиды

1. Если все боковые ребра равны, то около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр.

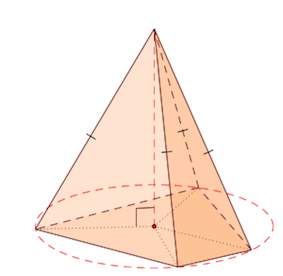
Боковые ребра образуют с плоскостью основания равные углы.

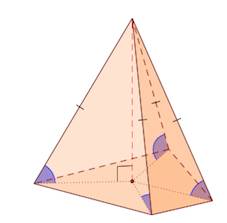
Верно и обратное.

Если боковые ребра образуют с плоскостью основания равные углы, то все боковые ребра пирамиды равны.

Если около основания пирамиды можно описать окружность, причем вершина пирамиды проецируется в ее центр, то все боковые ребра пирамиды равны.

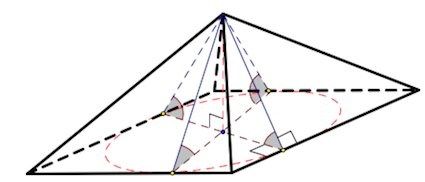
2. Если все грани пирамиды наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, причем вершина пирамиды проецируется в ее центр.

Виды пирамид

Пирамида называется правильной, если основанием ее является правильный многоугольник, а вершина проецируется в центр основания.

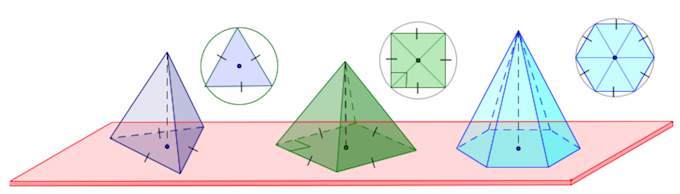
Для правильной пирамиды справедливо:

• боковые ребра правильной пирамиды равны;
• в правильной пирамиде все боковые грани – равные равнобедренные треугольники;
• в любую правильную пирамиду можно вписать сферу;
• около любой правильной пирамиды можно описать сферу;
• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

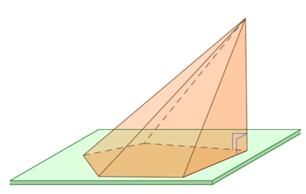
Пирамида называется прямоугольной, если одно из боковых ребер пирамиды перпендикулярно основанию. Тогда это ребро и есть высота пирамиды.

Усеченной пирамидой называется многогранник, заключенный между основанием пирамиды и секущей плоскостью, параллельной ее основанию.

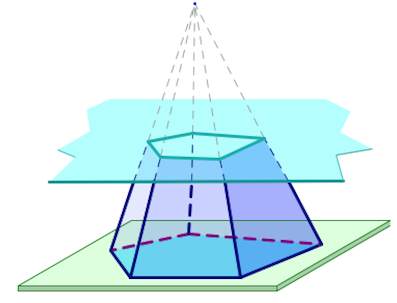
Усеченная пирамида является правильной, если она представляет собой часть правильной пирамиды.

Свойства усеченной пирамиды:

1. Каждая боковая грань правильной усеченной пирамиды является равнобокими трапециями одной величины.
2. Основания усеченной пирамиды являются подобными многоугольниками.
3. Боковые ребра правильной усеченной пирамиды имеют равную величину и один наклонен по отношению к основанию пирамиды.
4. Боковые грани усеченной пирамиды являются трапециями.
5. Двугранные углы при боковых ребрах правильной усеченной пирамиды имеют равную величину.

Тетраэдр – треугольная пирамида. В тетраэдре любая из граней может быть принята за основание пирамиды.

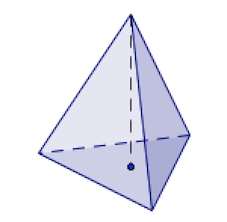
В правильном тетраэдре все четыре грани являются равносторонними треугольниками.

Соотношение между длиной ребра и высотой в правильном тетраэдре: \(h = a\sqrt {\large\frac{2}{3}}\normalsize\).