Конус. Усеченный конус

Конус или коническая поверхность представляет собой пространственную фигуру, образованную движением прямой, проходящей через некоторую определенную точку (вершину конуса) и пересекающую заданную линию, которая называется направляющей конуса. Указанная прямая называется образующей. Часто конусом называется пространственная фигура, ограниченная внутренней частью плоскости, пересекающей коническую поверхность, и частью конической поверхности, заключенной между вершиной и границей пересечения. Часть указанной плоскости, лежащая внутри конической поверхности, называется основанием конуса, а часть конической поверхности − боковой поверхностью.

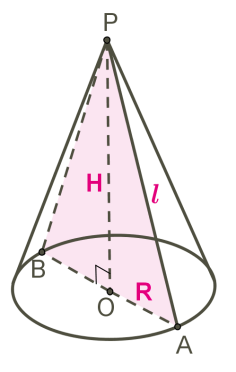Треугольник \(POA\) вращается вокруг стороны \(PO\). \(PO\) − ось конуса и высота конуса. \(P\) − вершина конуса. \(PA\) − образующая конуса. Круг с центром O − основание конуса. \(AO\) − радиус основания конуса. Осевое сечение конуса − это сечение конуса плоскостью, которая проходит через ось \(PO\) конуса. Осевое сечение конуса − это равнобедренный треугольник. \(APB\) − осевое сечение конуса. \(\angle PAO=\angle PBO\) − углы между образующими и основанием конуса.

Разверткой боковой поверхности конуса является круговой сектор. Длина дуги сектора − это длина окружности основания конуса длиной 2πR, угол развертки боковой поверхности α.

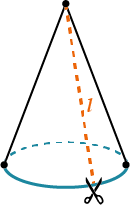
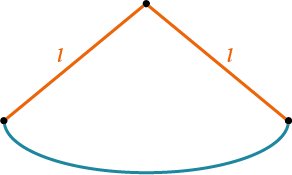
Конус называется круговым, если в его основании лежит круг.

Конус является прямым, если его вершина проецируется в центр основания.

Прямой круговой конус образуется при вращении прямоугольного треугольника вокруг его катета. Прямой круговой конус определяется радиусом основания R и высотой H (или радиусом основания R и образующей m).

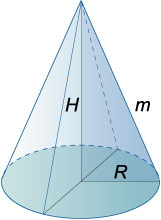
Соотношение между высотой, радиусом основания и образующей в прямом круговом конусе: \(H = \sqrt {{m^2} - {R^2}}\).

Площадь боковой поверхности прямого кругового конуса: \({S_{\text{бок}}} = \pi Rm\).

Площадь основания кругового конуса: \({S_{\text{осн}}} = \pi {R^2}\).

Площадь полной поверхности прямого кругового конуса: \(S = {S_{\text{бок}}} + {S_{\text{осн}}} = \pi R\left( {m + R} \right)\).

Объем кругового конуса: \(V = \large\frac{{{S_{\text{осн}}}H}}{3}\normalsize = \large\frac{{\pi {R^2}H}}{3}\normalsize\).

Если провести сечение конуса плоскостью, перпендикулярной оси конуса, то эта плоскость разбивает конус на две части, одна из которых − конус, а другую часть называют усеченным конусом.

Обычно под усеченным конусом имеется ввиду часть прямого кругового конуса. Такой усеченный конус образуется при вращении прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной основаниям трапеции. Усеченный конус определяется радиусами оснований R и r, высотой H (или, соответственно, образующей m).

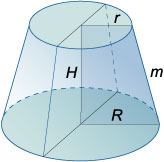
Соотношение между высотой, радиусами оснований и образующей в усеченном конусе: \(H = \sqrt {{m^2} - {{\left( {R - r} \right)}^2}}\).

Основания усеченного конуса подобны друг другу: \(\large\frac{R}{r}\normalsize = k\), где \(k\) − коэффициент подобия.

Отношение площадей нижнего и верхнего оснований: \(\large\frac{{{S_2}}}{{{S_1}}}\normalsize = \large\frac{{{R^2}}}{{{r^2}}}\normalsize = {k^2}\).

Площадь боковой поверхности усеченного конуса: \({S_{\text{бок}}} = \pi m\left( {R + r} \right)\).

Площадь полной поверхности усеченного конуса: \(S = {S_1} + {S_2} + {S_{\text{бок}}} = \pi \left[ {{R^2} + {r^2} + m\left( {R + r} \right)} \right]\).

Объем усеченного конуса: \(V = \large\frac{h}{3}\normalsize\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)\).