+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Цилиндр
Предыдущий конспект Следующий конспект
Конспект

Цилиндр − это геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Цилиндрическая поверхность образуется движением прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой, которая называется направляющей. Указанная прямая является образующей цилиндрической поверхности.

Прямоугольник \(AOO_1A_1\) вращается вокруг стороны \(OO_1\). \(OO_1\) − ось симметрии цилиндра и высота цилиндра.

\(AA_1\) − образующая цилиндра, длина которой равна длине высоты цилиндра.

\(AO\) − радиус цилиндра.

Полученная цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги − основаниями цилиндра.

Высотой цилиндра называется длина его образующей, а радиусом цилиндра называется радиус его основания.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Цилиндр называется круговым, если его направляющая является окружностью.

Цилиндр называется прямым, если его образующая перпендикулярна основаниям.

Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.

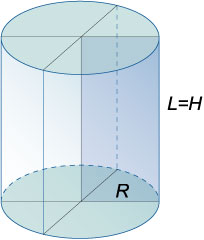
прямой круговой цилиндр

Если представить, что боковая цилиндрическая поверхность разрезана по образующей и развернута, получаем прямоугольник.

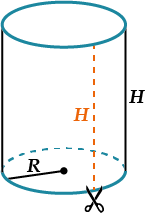
Развертка цилиндра Прямоугольник

Площадь боковой поверхности цилиндра: \({S_{\text{бок}}} = 2\pi RH\).

Площадь полной поверхности цилиндра: \(S = {S_{\text{бок}}} + 2{S_{\text{осн}}} = 2\pi R\left( {H + R} \right)\).

Объем цилиндра: \(V = {S_{\text{осн}}}H = \pi {R^2}H\).



Вопросы

  1. В цилиндре параллельно его оси проведено сечение, диагональ которого равна 17 см, высота цилиндра равна 15 см, а радиус основания – 5 см. На каком расстоянии от оси проведено это сечение?

  2. Высота цилиндра равна 3, а радиус основания – 2. Найдите площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной от нее на расстояние 1.

  3. В цилиндре высотой 5 и радиусом 6 проведено сечение, параллельное оси и отсекающее от окружности основания дугу в 120\(^\circ\). Определите площадь этого сечения.

  4. Площадь боковой поверхности цилиндра равна \(64 \pi\), а высота – 8. Найдите диаметр основания.

  5. Одна цилиндрическая кружка вдвое выше второй, зато вторая в полтора раза шире. Найдите отношение объема второй кружки к объему первой.

  6. Пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра равна \(40 \pi\), а диа­метр ос­но­ва­ния равен 5. Най­ди­те вы­со­ту ци­лин­дра.

  7. Длина окружности основания прямого цилиндра равна \(8π\) см, а диагональ осевого сечения – 17 см. Найдите образующую цилиндра.

  8. Чему равна площадь боковой поверхности цилиндра?

  9. Чему равна площадь полной поверхности цилиндра?

  10. Что представляет боковая поверхность цилиндра?

Сообщить об ошибке