Шар и сфера. Вписанные и описанные шары

Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.

Поверхность шара называется сферой. Сфера − это геометрическое место точек в пространстве, равноудаленных от некоторой заданной точки (центра сферы).

Площадь сферы: $S = 4\pi {R^2}$.

Объем шара: $V = {\large\frac{{4\pi {R^3}}}{3}\normalsize}$.

Шаровым сегментом называется часть шара, отсекаемая плоскостью.

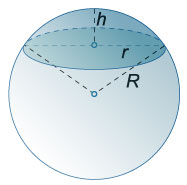
Соотношение между высотой и радиусом основания сегмента и радиусом шара: $R = \large\frac{{{r^2} + {h^2}}}{{2h}}\normalsize$, где $h$ − высота сегмента, $r$ − радиус основания сегмента, $R$ − радиус шара.

Площадь основания шарового сегмента: ${S_{\text{осн}}} = \pi {r^2}$.

Площадь внешней поверхности шарового сегмента: ${S_{\text{сегм}}} = \pi \left( {{h^2} + {r^2}} \right)$.

Площадь полной поверхности шарового сегмента: $S = {S_{\text{осн}}} + {S_{\text{сегм}}} = \pi \left( {{h^2} + 2{r^2}} \right) = \pi \left( {2Rh + {r^2}} \right)$.

Объем шарового сегмента: $V = \large\frac{{\pi {h^2}\left( {3R - h} \right)}}{6}\normalsize = \large\frac{{\pi h\left( {3{r^2} + {h^2}} \right)}}{6}\normalsize$.

Шаровым слоем называется часть шара, заключенная между двумя параллельными плоскостями.

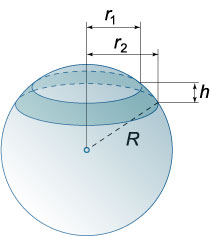
Площадь внешней поверхности шарового слоя: ${S_{\text{сл}}} = 2\pi Rh$, где $h$ − высота шарового слоя, $R$ − радиус шара.

Площадь полной поверхности шарового слоя: $S = {S_{\text{сл}}} + {S_1} + {S_2} = \pi \left( {2Rh + r_1^2 + r_2^2} \right)$, где $h$ − высота шарового слоя, $R$ − радиус шара, $r_1, r_2$ − радиусы оснований шарового слоя, $S_1, S_2$ − площади этих оснований.

Объем шарового слоя: $V = \large\frac{{\pi h\left( {3r_1^2 + 3r_2^2 + {h^2}} \right)}}{6}\normalsize$, где $r_1, r_2$ − радиусы оснований шарового слоя, $h$ − его высота.

Шаровым сектором называется часть шара, состоящая из шарового сегмента и конуса с вершиной в центре шара и основанием, совпадающим с основанием шарового сегмента. Здесь подразумевается, что шаровой сегмент меньше полушара.

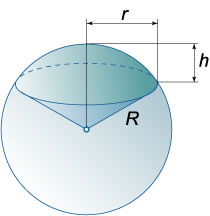
Площадь полной поверхности шарового сектора: $S = \pi R\left( {2h + r} \right)$, где $h$ − высота соответствующего шарового сегмента, $r$ − радиус основания шарового сегмента (или конуса), $R$ − радиус шара.

Объем шарового сектора: $V = \large\frac{{2\pi {R^2}h}}{3}\normalsize$.

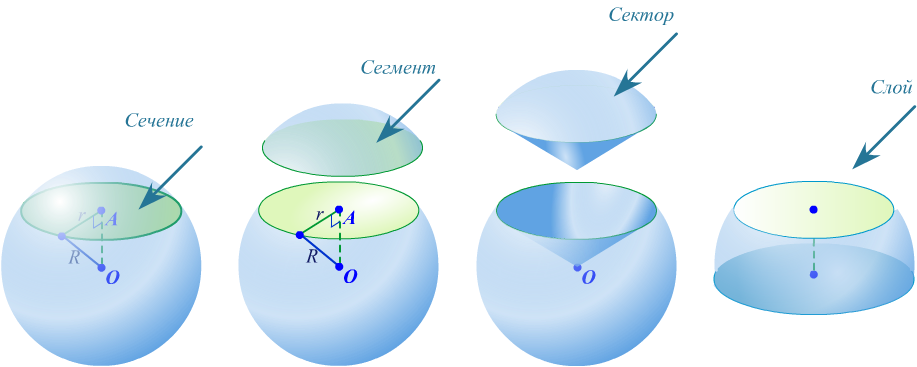
В геометрии часто рассматриваются разные комбинации геометрических тел с шаром. Для успешного решения таких задач важно сделать правильный чертеж, определить центр и радиус шара.

Шар и куб

Шар является описанным около куба, если все вершины куба находятся на поверхности шара.

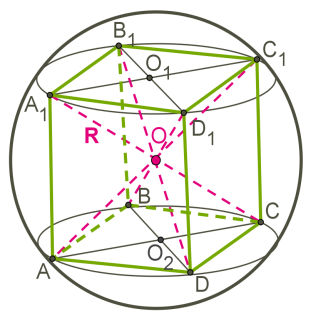
Центр шара O − точка пересечения диагоналей куба.

Около любого куба можно описать шар.

Общие точки шара и куба − восемь вершин куба.

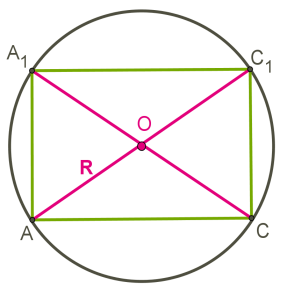
Чертится диагональное сечение.

AC₁ и CA₁ − диагонали куба.

Радиус шара равен половине диагонали куба.

Шар является вписанным в куб, если он касается всех его граней.

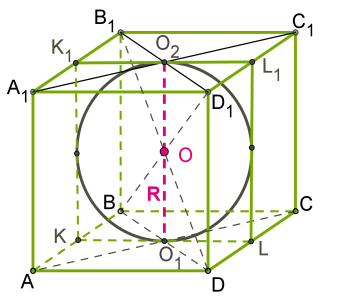
Центр шара O находится в точке пересечения диагоналей куба. В любой куб можно вписать шар. Общие точки шара и куба − центры шести граней куба (точки касания шара и куба).

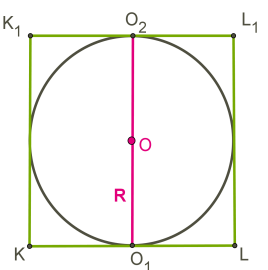
Чертится сечение плоскостью, которая параллельна грани куба и проходит через центр шара.

Радиус шара − половина стороны куба.

Шар и цилиндр

Шар является описанным около цилиндра, если окружности оснований цилиндра лежат на поверхности шара.

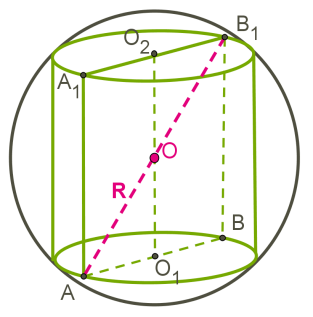
Центр шара O находится в середине высоты цилиндра.

Общие элементы − две окружности.

Около любого цилиндра можно описать шар.

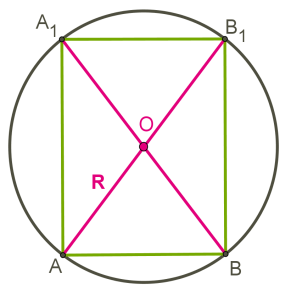
Чертится осевое сечение.

Радиус шара − половина диагонали осевого сечения цилиндра.

Шар является вписанным в цилиндр, если касается оснований цилиндра и всех его образующих.

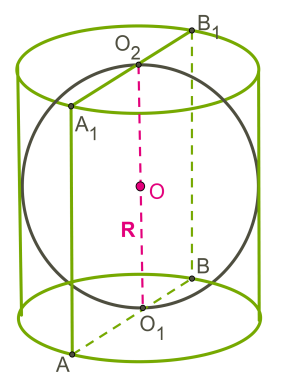
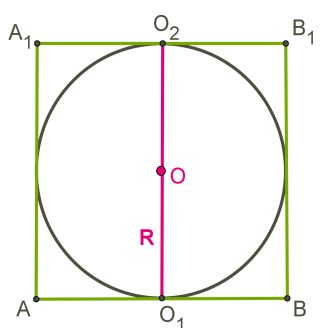
Центр шара O − середина высоты цилиндра.

Шар можно вписать только в такой цилиндр, в котором диаметр основания равен высоте.

Шар и конус

Шар является описанным около конуса, если вершина конуса и окружность его основания находятся на поверхности шара.

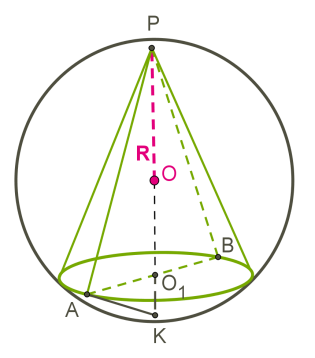
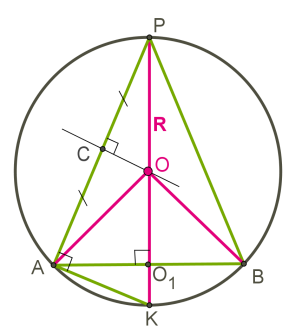
Около любого конуса можно описать шар.

Чертится осевое сечение.

В общем случае осевым сечением является равнобедренный треугольник.

Центр шара O находится в точке пересечения высоты конуса и серединного перпендикуляра образующей конуса.

Шар является вписанным в конус, если касается основания конуса и всех его образующих.

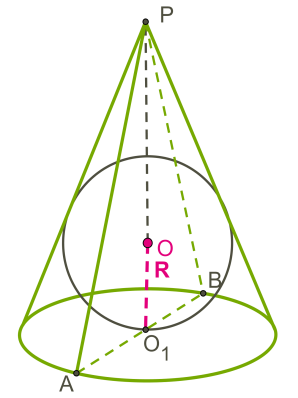
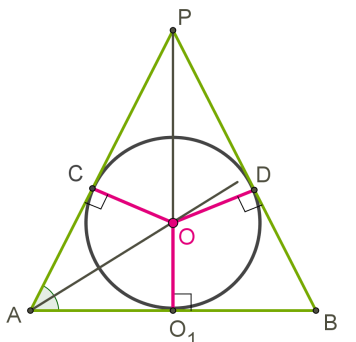
В любой конус можно вписать шар.

Чертится осевое сечение.

В общем случае осевым сечением является равнобедренный треугольник.

Центр шара O находится в точке пересечения высоты конуса и биссектрисы угла образующей конуса с основанием конуса.