+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Преобразование функции. Промежутки возрастания и убывания
Предыдущий конспект Следующий конспект
Конспект

С помощью операций преобразования графики некоторой функции \(y=f(x)\) можно превратить в график значительно более сложной функции без никаких вычислений. К операциям преобразования относятся:

  • параллельный перенос осей координат;
  • смена масштабов по осям координат;
  • смена ориентации осей координат;
  • преобразование абсолютных величин на графике.
Преобразование Описание Рисунок

\(y = f (x + c)\),

c – число

В случае \(c > 0\) график функции \(y = f (x)\) переносится влево на расстояние \(| c |\)

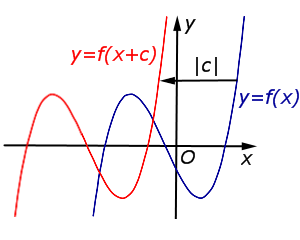 Элементарные преобразования графиков функций

В случае \(c < 0\) график функции \(y = f (x)\) переносится вправо на расстояние \(| c |\)

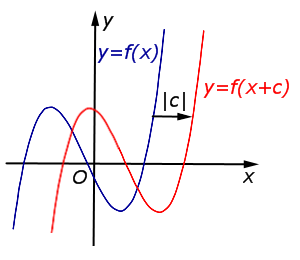 Элементарные преобразования графиков функций

\(y = f (x) + c\),

c – число

В случае \(c > 0\) график функции \(y = f (x)\) переносится вверх на расстояние \(| c |\)

 Элементарные преобразования графиков функций

В случае \(c < 0\) график функции \(y = f (x)\) переносится вниз на расстояние \(| c |\)

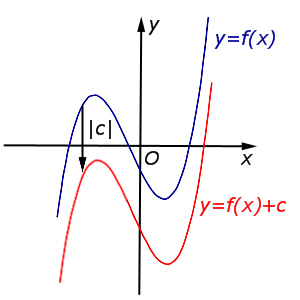 Элементарные преобразования графиков функций

\(y = – f (x)\)

График функции \(y = f (x)\) симметрично отражается относительно оси \(Ox\)

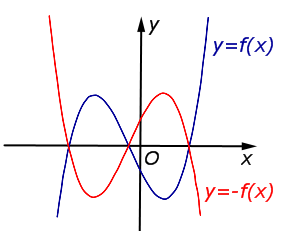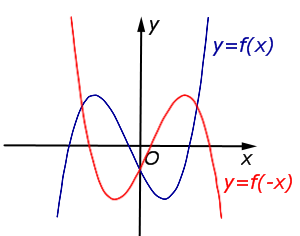
 Элементарные преобразования графиков функций

\(y = f ( – x)\)

График функции \(y = f (x)\) симметрично отражается относительно оси \(Oy\)

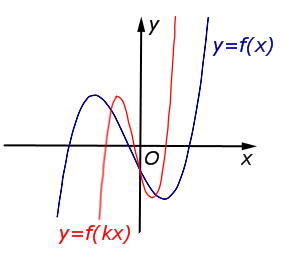
 Элементарные преобразования графиков функций

\(y = f (kx)\),

k – число

В случае \(k > 1\) происходит сжатие графика функции \(y = f (x)\) в \(k\) раз к оси \(Oy\)

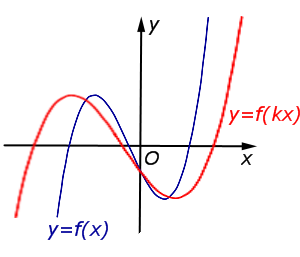
 Элементарные преобразования графиков функций

В случае \(0 < k < 1\) происходит растяжение графика функции \(y = f (x)\) в \(\frac1{k}\) раз от оси \(Oy\)

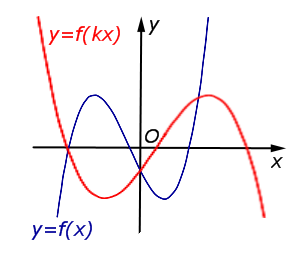
 Элементарные преобразования графиков функций

В случае \(– 1 < k <0\) происходит растяжение графика функции \(y = f (x)\) в \(\frac1{|k|}\) раз от оси \(Oy\) c последующим симметричным отражением графика относительно оси \(Oy\)

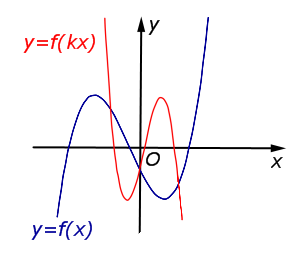
 Элементарные преобразования графиков функций

В случае \(k < – 1\) происходит сжатие графика функции \(y = f (x) \ в \ | k |\) раз к оси \(Oy\) с последующим симметричным отражением графика относительно оси \(Oy\)

 Элементарные преобразования графиков функций

\(y = k f (x)\),

k – число

В случае \(k > 1\) происходит растяжение графика функции \(y = f (x) \ в\ k\) раз от оси \(Ox\)

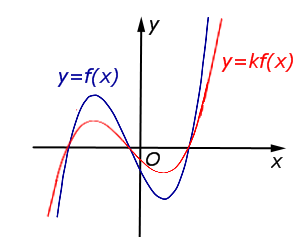
 Элементарные преобразования графиков функций

В случае \(0 < k < 1\) происходит сжатие графика функции \(y = f (x) \ в \ \frac1{k}\) раз к оси \(Ox\)

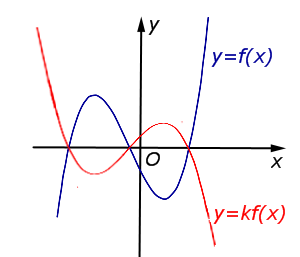
 Элементарные преобразования графиков функций

В случае \(– 1 < k < 0\) происходит сжатие графика функции \(y = f (x) \ в \ \frac1{|k|}\) раз к оси \(Ox\) с последующим симметричным отражением графика относительно оси \(Ox\)

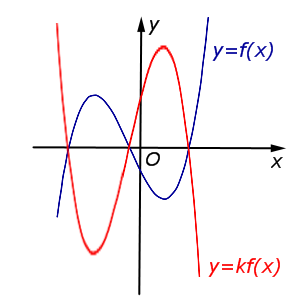
 Элементарные преобразования графиков функций

В случае \(k < – 1\) происходит растяжение графика функции \(y = f (x) \ в\ | k |\) раз от оси \(Ox\) с последующим симметричным отражением графика относительно оси \(Ox\)

 Элементарные преобразования графиков функций

\(y = | f (x)|\)

Часть графика функции \(y = f (x)\), расположенная в области \(y\ge0\), остается на месте. Часть графика функции \(y = f (x)\), расположенная в области \(y < 0\), симметрично отражается относительно оси \(Ox\)

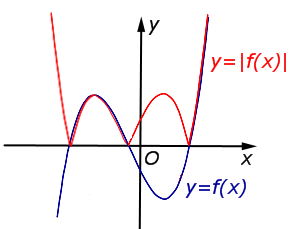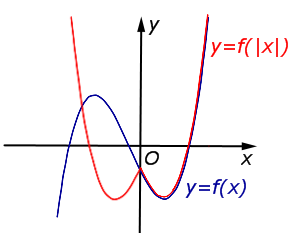
 Элементарные преобразования графиков функций

\(y = f (| x|)\)

Ось \(Oy\) является осью симметрии графика функции \(y = f (| x|)\). Часть графика функции \(y = f (x)\), расположенная в области \(x\ge0\), остается на месте. Часть графика функции \(y = f (| x|)\), расположенная в области \(x < 0\), получается из части графика, расположенной в области \(x\ge 0\) при помощи симметричного отражения относительно оси \(Oy\)

 Элементарные преобразования графиков функций

 

Функции, у которых имеет место убывание или возрастание на некотором числовом промежутке, называются монотонными функциями.

Возрастание функции. Функция называется возрастающей на интервале \([a;b]\), принадлежащем области определения функции, если большим значениям независимой переменной из этого интервала соответствуют большие значения функции, т. е. если \(x_2>x_1 \Rightarrow f(x_2)>f(x_1)\) для всех \(x_1\ и \ x_2\), принадлежащих интервалу.

Убывание функции. Функция называется убывающей на интервале \([a;b]\), если большим значениям независимой переменной из этого интервала соответствуют меньшие значения функции, т. е. если \(x_2>x_1 \Rightarrow f(x_2)\) для всех \(x_1 \ и \ x_2\), принадлежащих интервалу.

Теорема 1. Если во всех точках некоторого промежутка \(f'(x)=0\), то функция \(f(x)\) сохраняет в этом промежутке постоянное значение.

Этот промежуток может быть замкнутым или открытым, конечным или бесконечным.

Теорема 2 (достаточный признак возрастания). Если во всех точках некоторого промежутка \(f'(x)>0\), то функция \(f(x)\) возрастает в этом промежутке.

Теорема 3 (достаточный признак убывания). Если во всех точках некоторого промежутка \(f'(x)<0\), то \(f(x)\) убывает на этом промежутке.

Замечание. Условия теорем 2 и 3 не являются в полной мере необходимыми. Их можно несколько ослабить, а именно считать, что \(f'(x)\ge0\) или \(f'(x)\le0\), так как заключения теорем остаются справедливыми и тогда, когда производная обращается в нуль в конечном множестве точек.



Вопросы

  1. Найдите промежутки убывания функции.

    \(y=10x\cdot e^{-x}\)

  2. Найдите промежутки возрастания функции.

    \(y=2lnx-x^2\)

  3. Найдите промежутки убывания функции.

    \(\frac{1-x}{(x-2)^3}\)

  4. Найдите промежутки возрастания функции.

    \(f(x)=\frac{3x}{x^2+4x+4}\)

  5. Найдите промежутки убывания функции.

    \(f(x)=x^3+6x^2+9x\)

  6. Найдите промежутки а) возрастания и б) убывания функции.

    \(y=\frac{x^3}3-\frac{x^2}2-2x+3\)

Сообщить об ошибке