Виды функции. Обратная функция. Область определения и область значения функции

Понятие функции является одним из основных в математике. Оно вводится следующим образом.

Пусть заданы два множества \(X\) и \(Y\). Если каждому элементу \(x\) из множества \(X\) поставлен в соответствие элемент \(y=f(x)\) множества \(Y\), то говорят, что на множестве \(X\) задана функция \(f\). При этом элемент \(x\) называется независимой переменной, а элемент \(y\) − зависимой переменной. В случае, когда \(x\ и \ y\) являются действительными числами, функцию \(y=f(x)\) можно представить в виде графика в декартовой системе координат \(Oxy\).

Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, то есть по оси абсцисс откладываются значения переменной \(x\), а по оси ординат откладываются значения переменной \(y\).

Область определения функции \(D(y)\) – это множество всех допустимых значений аргумента \(x\), при которых выражение, стоящее в правой части уравнения функции \(y=f(x)\), имеет смысл. Другими словами, это область допустимых значений выражения \(f(x)\).

Чтобы по графику функции \(y=f(x)\) найти ее область определения, нужно, двигаясь слева направо вдоль оси ОХ, записать все промежутки значений \(x\), на которых существует график функции.

Пример 1. Найти область определения функции: \(y=\sqrt{4x-x^3}\).

Решение: Поскольку квадратный корень можно извлекать только из неотрицательных чисел, то область определения данной функции задается неравенством \(4x-x^3\ge0 \Leftrightarrow x^3-4x\le0 \Rightarrow x(x-2)(x+2)\le0\).

Решая это неравенство с помощью метода интервалов, получим: \(x\in (-\infty; -] \cup [0;2]\).

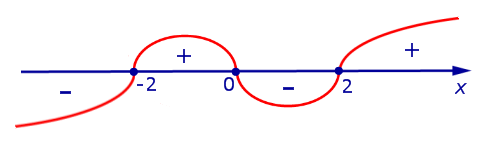
Ответ: \(x\in (-\infty; -] \cup [0;2]\).

Множество значений функции \(E(y)\) – это множество всех значений, которые может принимать зависимая переменная \(y\).

Чтобы по графику функции \(y=f(x)\) найти ее множество значений, нужно, двигаясь снизу вверх вдоль оси OY, записать все промежутки значений \(y\), на которых существует график функции.

Пример 2. Найти множество значений функции: \(y = x^2 + 6x + 8\).

Решение: Поскольку \(y=x^2+6x+8=x^2+6x+9-1=(x+3)^2-1\ge-1\) и для каждого числа \(y\ge-1\) существуют решения уравнения \(x^2 + 6x + 8 = y\), определяемые формулой \(x_{1,2}=-3\pm \sqrt{y+1}\), то множеством значений функции \(  y = x^2 + 6x + 8\) будет множество \([-1;+\infty)\).

Ответ: \(y\in [-1;+\infty)\).

Обратная функция

Пусть задана функция \(y=f(x)\). Чтобы найти обратную для нее функцию, надо из уравнения \(y=f(x)\) выразить переменную \(x\) через \(y\) и затем поменять переменные местами. Обратную функцию часто обозначают в виде \(y=f^{−1}(x)\). Исходная и обратная функции симметричны относительно прямой \(y=x\).

Чтобы для данной функции \(y = f(x)\) найти обратную, надо:

1. В соотношении \(y = f(x)\) заменить \(x\) на \(y\), а \(y\) на \(x\):  \(x = f(y)\).
2. В полученном выражении \(x=f(y)\) выразить \(y\) через \( x\).

Например, \(y=3x-8: x=3y-8 \Rightarrow 3y=x+8 \Rightarrow y=\frac{x+8}3\).

Свойства взаимно обратных функций

Тождества. Пусть \(f\) и \(g\) – взаимно обратные функции. Это означает, что равенства \(y = f(x)\) и \(x = g(y)\) равносильны. Подставим одно из этих равенств в другое. Получим два тождества: \(f(g(y)) = y\) и \(g(f(x)) = x\).

Область определения. Пусть \(f\) и \(g\) – взаимно обратные функции. Область определения функции \(f\) совпадает с областью значений функции \(g\), и наоборот, область значений функции \(f\) совпадает с областью определения функции \(g\).

Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное верно и для убывающих функций.

Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой \(y = x\).