+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Формулы приведения
Предыдущий конспект Следующий конспект
Конспект

Формулы приведения тригонометрических функций упрощают вид формул и помогают совершать преобразования, приводящие к более простым выражениям. Формулы приведения – приведенные ниже формулы, дающие возможность находить численные значения тригонометрических функций углов, превышающих 90°.

Формулы приведения можно сформулировать в виде следующего правила:

  • Если в формуле приведения угол вычитается (прибавляется) из 90° или 270°, то приводимая функция меняется на кофункцию.
  • Если же в формуле приведения угол вычитается (прибавляется) из 180° или 360°, то название приводимой функции сохраняется.
  • При этом перед приведенной функцией ставится тот знак, который имеет приводимая (т. е. исходная) функция в соответствующей четверти, если считать вычитаемый (прибавляемый) угол острым.

Формулы приведения задаются в виде таблицы:

Таблица Тригонометрические формулы приведения

Пример. Вы­чис­лить зна­че­ния всех три­го­но­мет­ри­че­ских функ­ций угла \(\alpha=\frac{7\pi}6=210^\circ\).

Ре­ше­ние:

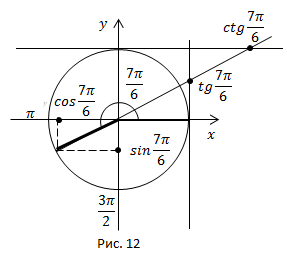
Угол 210° на­хо­дит­ся в тре­тьей чет­вер­ти, в тре­тьей чет­вер­ти синус и ко­си­нус от­ри­ца­тель­ны, тан­генс и ко­тан­генс по­ло­жи­тель­ны.

\(sin\frac{7\pi}6=sin(\pi+\frac{\pi}6)=-sin\frac{\pi}6=-\frac12; \\ cos\frac{7\pi}6=cos(\pi+\frac{\pi}6)=-cos\frac{\pi}6=-\frac{\sqrt3}2; \\tg\frac{7\pi}6=tg(\pi+\frac{\pi}6)=tg\frac{\pi}6=\frac1{\sqrt3}; \\\\ctg\frac{7\pi}6=ctg(\pi+\frac{\pi}6)=ctg\frac{\pi}6=\sqrt3.\)



Вопросы

  1. Упро­стите вы­ра­же­ние.

    \(\frac{tg(\pi-\beta)\cdot cos(\pi-\beta)\cdot tg(\frac{\pi}2-\beta)}{sin(\frac{\pi}2-\beta)\cdot ctg(\frac{\pi}2+\alpha)\cdot tg(\frac{3\pi}2+\alpha)}\)

     

  2. Упростите выражение.

    \(ctg(90^\circ-\alpha)[cos(360^\circ+\alpha)-sin\alpha]+\frac{sin\alpha+tg\alpha}{\frac1{sin\alpha}+ctg\alpha}\)

  3. Найдите значение выражения.

    \(\frac{5cos41^\circ}{sin131^\circ\cdot cos 240^\circ}\)

  4. Упростите выражение.

    \(tg(\frac{3\pi}2-\alpha)\cdot tg(\pi+\alpha)-cos(\frac{\pi}2+\alpha)\cdot sin(\pi+\alpha)\)

  5. Упростите выражение.

    \(\frac{tg(\pi-\alpha)\cdot cos(-\alpha)}{sin(\frac{\pi}2-\alpha)}\)

  6. Вычислите.

    \(sin(-960°)\)

  7. Упростите.

    \(\frac{2cos^2\alpha}{1-sin\alpha}+2cos(\frac{\pi}2+\alpha)\)

  8. Найдите значение выражения.

    \(tg(\frac{3\pi}2-1)\cdot sin(\pi-1)+cos(\pi+1)\)

  9. Bычислите.

    \(ctg 40^{\circ}\cdot tg140^{\circ}  \)

  10. Какому промежутку принадлежит значение выражения sinα – 3\(\pi^2\)(1 + tg2(α-\(\pi\))) при α=2\(\pi^3\)?

Сообщить об ошибке