Тригонометрические функции, их графики и свойства

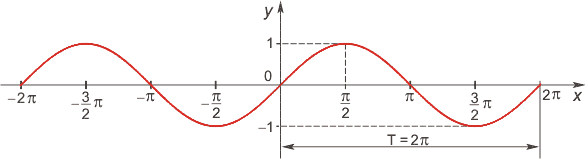
Функция $y=sinx$

• Область определения функции – множество всех действительных чисел: $D(y)=\mathbb R$.
• Множество значений: $E(y) = [−1;1]$.
• Функция $y=sinx$ нечетная: $sin(−x)=−sinx$.
• Функция оказывается периодической, самый маленький неотрицательный период соответствует $2π: sin(x+2π)=sinx$.
• График функции симметричен относительно начала координат.
• График функции пересекает ось $OX$ при $x=πk, k\in \mathbb Z$.
• Промежутки знакопостоянства: $sinx>0 \ при\ x\in (2πk+0;π+2πk),k\in \mathbb Z; \\ sinx<0\  при \ x\in (π+2πk;2π+2πk),k\in \mathbb Z.$
• Функция является непрерывной и у нее есть производная с любым значением аргумента: $(sinx)′=cosx$.
• Функция $y=sinx$ возрастает при $x\in(−\frac{π}2+2πk;\frac{π}2+2πk),k\in \mathbb Z$, и убывает при $x\in(\frac{π}2+2πk;\frac{3π}2+2πk),k\in \mathbb Z$.
• Минимум функции при $x=−\frac{\pi}2+2πk, k\in \mathbb Z$, а максимум при $x=\frac{\pi}2+2πk, k\in \mathbb Z$.

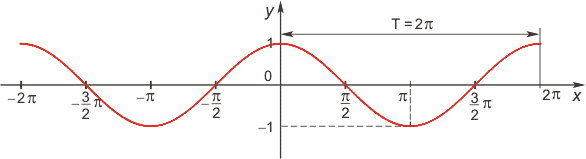
Функция $y=cosx$

• Область определения функции – множество всех действительных чисел: $D(y)=\mathbb R$, кроме $x= \frac{\pi}2+\pi k, k\in \mathbb Z$.
• Множество значений: $E(y) =[-1;1]$.
• Функция $y=cosx$ четная: $cos(−x)=cosx$.
• Функция оказывается периодической, самый маленький неотрицательный период соответствует $2π: cos(x+2π)=cosx$.
• График функции симметричен относительно оси OY.
• График функции пересекает ось $OX$ при $x=\frac{\pi}2+πk, k\in \mathbb Z$.
• Промежутки знакопостоянства: $cosx>0 \ при\ x\in (-\frac{\pi}2+2πk;\frac{π}2+2πk),k\in \mathbb Z; \\ cosx<0\  при \ x\in (\frac{π}2+2πk;\frac{3π}2+2πk),k\in \mathbb Z.$
• Функция является непрерывной, и у нее есть производная с любым значением аргумента: $(cosx)′=sinx$.
• Функция $y=cosx$ возрастает при $x\in[−{π}+2πk;2πk], k\in \mathbb Z$, и убывает при $x\in[2πk;π+2πk],k\in \mathbb Z$.
• Минимум функции при $x=\pi+2πk, k\in \mathbb Z$, а максимум при $x=2πk, k\in \mathbb Z$.

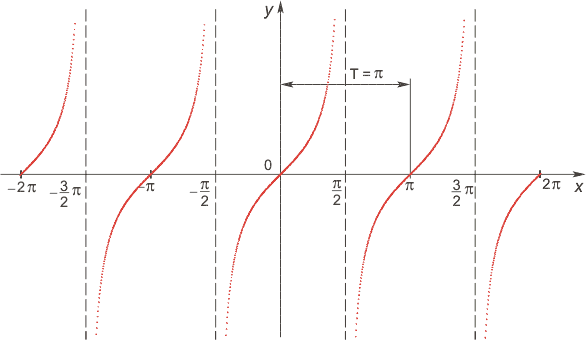
Функция $y=tgx$

• Область определения функции – множество всех действительных чисел: $D(y)=\mathbb R$, кроме $x= \frac{\pi}2+\pi k, k\in \mathbb Z$.
• Множество значений – множество действительных чисел: $E(y) = \mathbb R$.
• Функция $y=tgx$ нечетная: $tg(−x)=-tgx$.
• Функция оказывается периодической, самый маленький неотрицательный период соответствует $π: tg(x+π)=tgx$.
• График функции симметричен относительно оси OY.
• График функции пересекает ось $OX$ при $x=πk, k\in \mathbb Z$.
• Промежутки знакопостоянства: $tgx>0 \ при\ x\in (πk;\frac{π}2+πk),k\in \mathbb Z; \\ tgx<0\  при \ x\in (-\frac{π}2+πk;πk),k\in \mathbb Z.$
• Функция является непрерывной, есть производная с любым значением аргумента из области определения: $(tgx)′=\frac1{cos^2x}$.
• Функция $y=tgx$ возрастает при $x\in (−\frac{π}2+πk;\frac{π}2+πk), k\in \mathbb Z$.

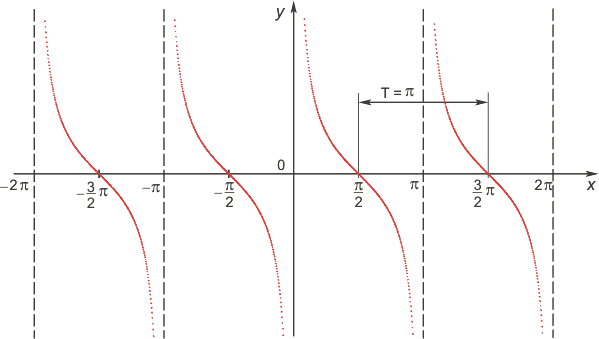
Функция $y=ctgx$

• Область определения функции – множество всех действительных чисел: $D(y)=\mathbb R$, кроме $x= \pi k, k\in \mathbb Z$.
• Множество значений – множество действительных чисел: $E(y) = \mathbb R$.
• Функция $y=ctgx$ нечетная: $ctg(−x)=-ctgx$.
• Функция оказывается периодической, самый маленький неотрицательный период соответствует $π: ctg(x+π)=ctgx$.
• График функции симметричен относительно оси OY.
• График функции пересекает ось $OX$ при $x=\frac{\pi}2+πk, k\in \mathbb Z$.
• Промежутки знакопостоянства: $ctgx>0 \ при\ x\in (πk;\frac{π}2+πk),k\in \mathbb Z; \\c tgx<0\  при \ x\in (-\frac{π}2+πk;πk),k\in \mathbb Z.$
• Функция является непрерывной, есть производная с любым значением аргумента из области определения: $(ctgx)′=-\frac1{sin^2x}$.
• Функция $y=ctgx$ убывает при $x\in (πk;π+πk), k\in \mathbb Z$.