+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Синус, косинус, тангенс, котангенс произвольного угла
Предыдущий конспект Следующий конспект
Конспект

Чтобы ввести определения синуса, косинуса, тангенса и котангенса для произвольного угла, воспользуемся тригонометрической окружностью.

Рассмотрим прямоугольный треугольник AOP. По определению тригонометрических функций острого угла, имеем:

\(sin\alpha=\frac{AP}{OP}, \ cos\alpha=\frac{OA}{OP}, \ tg\alpha=\frac{AP}{OA}, \ ctg\alpha=\frac{OA}{AP}\). Но \(OA=x, AP=y, OP=R\). Отсюда, \(sin\alpha=\frac{y}{R}, \ cos\alpha=\frac{x}{R}, \ tg\alpha=\frac{y}{x}, \ ctg\alpha=\frac{x}{y}\).

Изменение радиуса окружности не влияет на значения синуса и косинуса. Поэтому удобно выбрать R = 1. Такую окружность называют единичной. Таким образом, \(sin\alpha=y, \ cos\alpha=x\).

Чаще всего единичная окружность используется для определения знака тригонометрической функции, числовые значения находятся в таблицах или вычисляются с помощью калькулятора.

Значения тригонометрических функций, которые нужно знать наизусть.

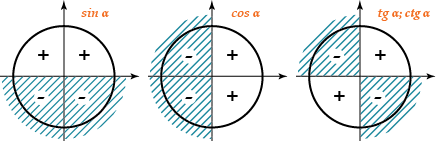
Взяв произвольный угол \(\alpha\) и пройдя полностью всю окружность, мы вернемся в тот же самый угол \( α\).

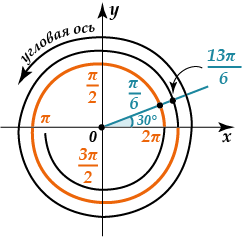
углы больше 360 на тригонометрической окружности

\(sin(α+2πk)=sinα \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ tg(α+πk)=tg α \\cos(α+2πk)=cosα \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ ctg(α+πk)=ctg α\)

Синус и косинус являются периодическими функциями с периодом 2π.

Тангенс и котангенс являются периодическими функциями с периодом π.



Вопросы

  1. Если \(cos\alpha=\frac23, \ 0\leq\alpha\leq\frac{\pi}2\), то вычислите значение \(ctg\alpha\).

  2. Вычислите.

    \(cos\frac{43 \pi}6\)

  3. Вычислите.

    \(sin90°\)

  4. Вычислите.

    \(sin 810°\)

  5. Вычислите.

    \(ctg1140°\)

  6. Вычислите.

    \(sin300° \)

  7. Если \(cos\alpha=\frac23, \ 0\leq\alpha\leq\frac{\pi}2\), то вычислите значение \(sin\alpha\).

  8. Если \(cos\alpha=\frac23, \ 0\leq\alpha\leq \frac{\pi}2\), то вычислите значение \(tg\alpha\).

  9. Вычислите значение выражения.

    \(-sin990^\circ\)

  10. Найдите числовое значение выражения.

    \(5sin\frac{3\pi}6\)

Сообщить об ошибке