Вписанные и описанные окружности

Окружность называется описанной около многоугольника, если она проходит через все его вершины. Центр описанной окружности лежит в точке пересечения серединных перпендикуляров, проведенных к сторонам многоугольника.

Окружность называется вписанной в многоугольник, если она касается всех сторон многоугольника. Центр вписанной окружности лежит в точке пересечения биссектрис углов многоугольника.

Правильным многоугольником называется выпуклый многоугольник с равными сторонами и равными углами.

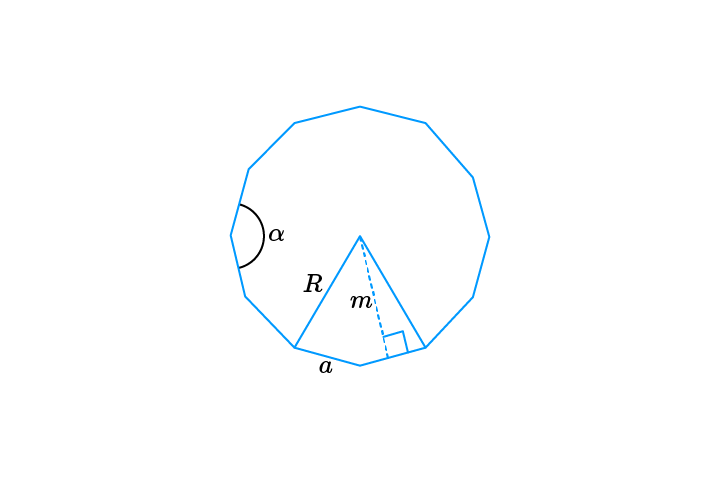
• Внутренние углы в правильном многоугольнике равны между собой и определяются выражением \(\alpha = \large\frac{{n - 2}}{n}\normalsize \cdot 180^\circ\), где \(n\) − число сторон.
• Радиус описанной окружности: \(R = \large\frac{a}{{2\sin \frac{\pi }{n}}}\normalsize\).
• Радиус вписанной окружности правильного многоугольника совпадает с апофемой (перпендикуляром, опущенным из центра на любую сторону) и выражается формулой \(r = m = \large\frac{a}{{2\tan \frac{\pi }{n}}}\normalsize = \sqrt {{R^2} - \large\frac{{{a^2}}}{4}}\normalsize\), где \(r\) − радиус вписанной окружности, \(m\) − апофема, \(R\) − радиус описанной окружности, \(a\) − сторона многоугольника.
• Периметр правильного многоугольника: \(P = na\).
• Площадь правильного многоугольника: \(S = \large\frac{{n{R^2}}}{2}\normalsize\sin \large\frac{{2\pi }}{n}\normalsize; \ S = pr = p\sqrt {{R^2} - \large\frac{{{a^2}}}{4}}\normalsize\).

Треугольник, вписанная и описанная около него окружность

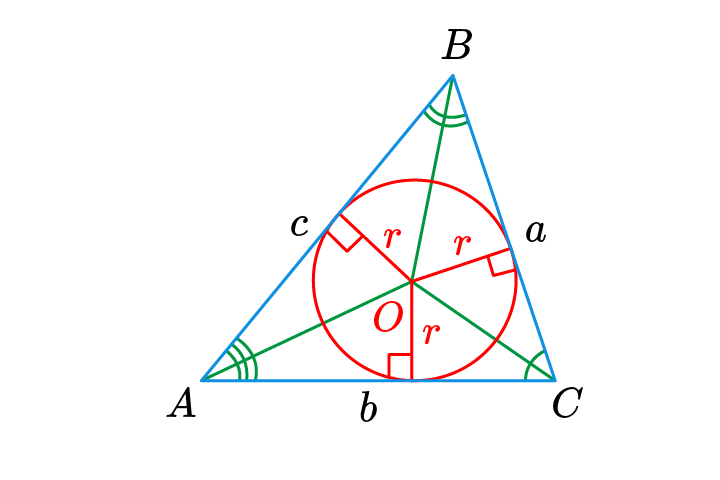
\(a, b, c\) – стороны треугольника, \(S\) – площадь, \(r\) – радиус вписанной окружности, \(p\) – полупериметр.

\(p=\frac{a+b+c}{2}; \ r=\frac{S}{p}=\frac{2S}{a+b+c}; \ r=\sqrt{\frac{(p-a)(p-b)(p-c)}{p}}\).

\(a\) – боковая сторона равнобедренного треугольника, \(b\) – основание, \(r\) – радиус вписанной окружности.

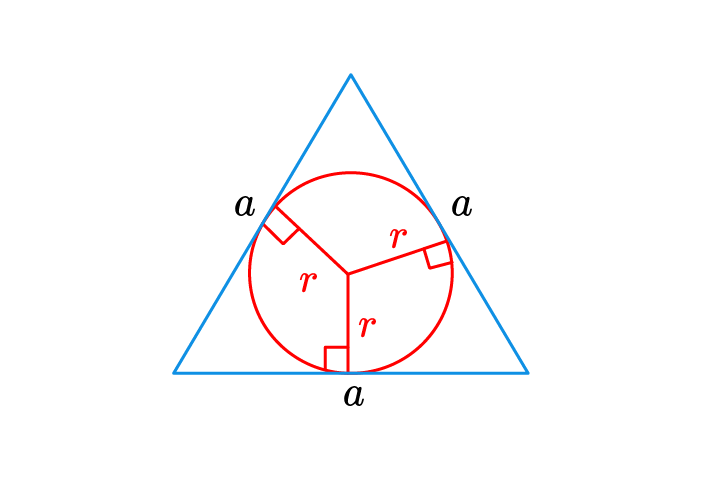
\(a\) – сторона равностороннего треугольника, \(r\) – радиус вписанной окружности.

\(r=\frac{a\sqrt3}{6}; \ R=\frac{a}{\sqrt3}\).

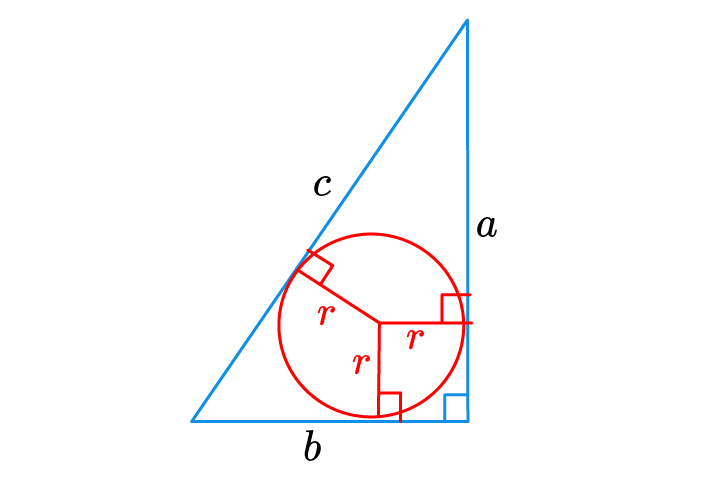
\(r=\frac{a+b-c}2\).

Для любого треугольника справедливо равенство: \(S = 2R^2 sin \angle A sin \angle B sin\angle C\), где \(A, B, C\) – углы треугольника, \(S\) – площадь треугольника, \(R\) – радиус описанной окружности.

Для любого треугольника справедливо равенство: \(R=\frac{abc}{4S}\), где \(a, b, c\) – стороны треугольника, \(S\) – площадь треугольника, \(R\) – радиус описанной окружности.

Квадрат, вписанная и описанная около него окружность

Пусть а – это сторона квадрата, радиус описанной окружности равен R, а радиус вписанной окружности равен r.

Стороны квадрата и вписанная в него окружность имеют общие точки (точки касания), эти точки делят стороны квадрата пополам.

Радиус описанной окружности, проведенный к вершине квадрата, является биссектрисой, то есть делит угол квадрата пополам.

\(a=2r \Rightarrow r=\frac{a}2;\ a=R\sqrt2 \Rightarrow R=\frac{a}{\sqrt2}; \ r=\frac{R\sqrt2}2\).

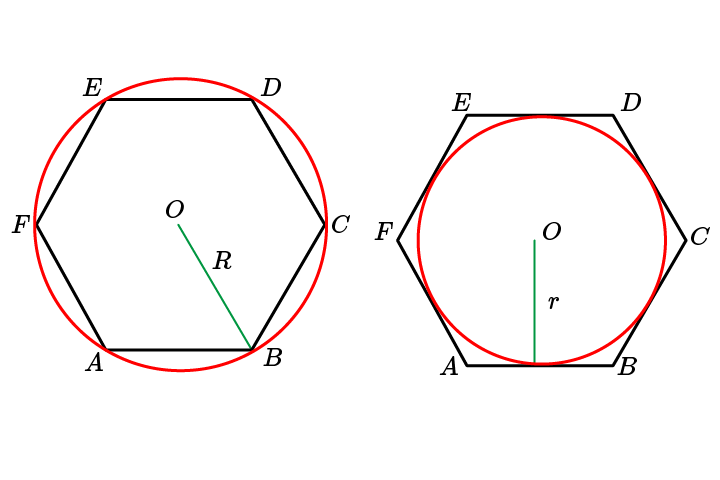
Правильный шестиугольник, вписанная и описанная около него окружность

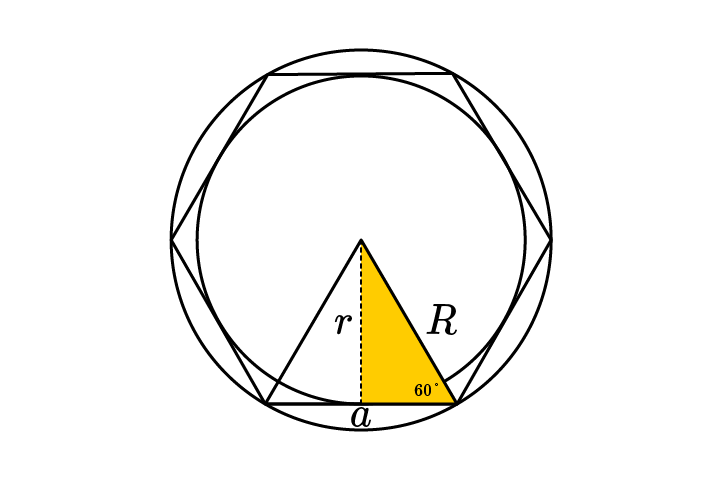
Стороны правильного шестиугольника и вписанная окружность имеют общие точки (точки касания), эти точки делят стороны данного шестиугольника пополам.

Радиус описанной окружности, проведенный к вершине шестиугольника, является биссектрисой, то есть делит угол правильного шестиугольника, равный 120°, пополам.

\(a=\frac{2r}{\sqrt3} \ \Rightarrow r=\frac{a\sqrt3}2; \ R=\frac{2r}{\sqrt3} \Rightarrow r=\frac{R\sqrt3}2\).