Площадь криволинейной трапеции

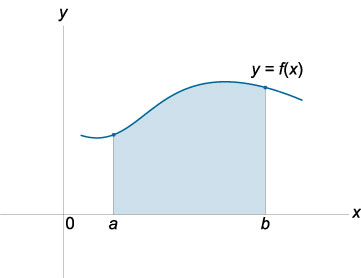
Рассмотрим непрерывную функцию $y = f ( x )$, заданную на отрезке $[ a; b ]$ и сохраняющую на этом отрезке свой знак. Фигура, ограниченная графиком этой функции, отрезком $[ a;b ]$ и прямыми $x = a \ и \ x = b$, называется криволинейной трапецией.

Для вычисления площадей криволинейных трапеций используется следующая теорема:

Если $f(x)$ – непрерывная, неотрицательная функция на отрезке $[a;b] \ и \ F(x)$ – ее первообразная на этом отрезке, то площадь соответствующей криволинейной трапеции равна приращению первообразной на отрезке $[a; b]$, т. e. $S=F(b)-F(a)$.

Площадь криволинейной трапеции, ограниченной графиком непрерывной положительной на промежутке $[ a ; b ]$ функции $f (x)$ осью $Ox$ и прямыми $x=a \ и\ x= b$:

$S = \int\limits_a^b {f\left( x \right)dx} = F\left( b \right) - F\left( a \right)$.

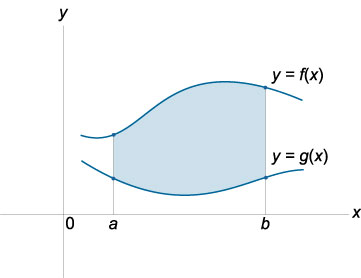
Площадь фигуры, ограниченной кривыми $y=f(x)\ и \ y=g(x),  [f(x) \ge g(x)]$ и прямыми $x=a, x=b$, вычисляется по формуле ${S = \int\limits_a^b {\left[ {f\left( x \right) - g\left( x \right)} \right]dx} } = {F\left( b \right) - G\left( b \right) - F\left( a \right) + G\left( a \right)}$.

Пример. Найти площадь фигуры, ограниченной графиками функций $y = 2x - {x^2}$ и $x + y = 0$.

Решение:

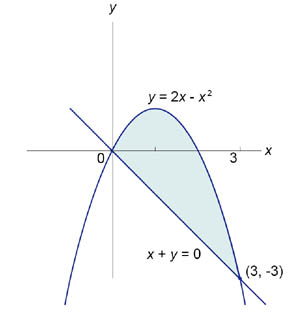
Найдем координаты точек пересечения кривых: ${2x - {x^2} = - x}\;\; {\Rightarrow {x^2} - 3x = 0}\;\; {\Rightarrow x\left( {x - 3} \right) = 0}\;\; {\Rightarrow {x_1} = 0,\;{x_2} = 3}$.

Данная область ограничивается сверху параболой $y=2x−x^2$, а снизу − прямой линией $y=−x$. Следовательно, площадь этой области равна:

${S = \int\limits_0^3 {\left[ {2x - {x^2} - \left( { - x} \right)} \right]dx} } = {\int\limits_0^3 {\left( {2x - {x^2} + x} \right)dx} } = {\left. {\left( {{x^2} - \frac{{{x^3}}}{3} + \frac{{{x^2}}}{2}} \right)} \right|_0^3 }= \\= {\left. {\left( {\frac{{3{x^2}}}{2} - \frac{{{x^3}}}{3}} \right)} \right|_0^3 } = {\frac{{27}}{2} - \frac{{27}}{3} = \frac{9}{2}.}$