Неопределенный интеграл

Функция \(F(x)\) называется первообразной функции \( f(x)\), если \(F'\left( x \right) = f\left( x \right)\).

Множество всех первообразных некоторой функции \(f(x)\) называется неопределенным интегралом функции \(f(x)\) и обозначается как \(\int {f\left( x \right)dx} \). Таким образом, если \(F\) – некоторая частная первообразная, то справедливо выражение \(\int {f\left( x \right)dx} = F\left( x \right) + C,\) где \(C\) – произвольная постоянная. Функция \(f(x)\) называется подынтегральной функцией, а выражение \(f(x)dx\) – подынтегральным выражением.

Свойства неопределенного интеграла

В приведенных ниже формулах \(f \ и \ g \) – функции переменной \(x\), \(F\) – первообразная функции \(f\) и \(a,k,C\) − постоянные величины.

• \(\int {\left[ {f\left( x \right) + g\left( x \right)} \right]dx} = \int {f\left( x \right)dx} + \int {g\left( x \right)dx}\)
• \(\int {kf\left( x \right)dx} = k\int {f\left( x \right)dx}\)
• \(\int {f\left( {ax} \right)dx} = {\large\frac{1}{a}\normalsize} F\left( {ax} \right) + C\)
• \(\int {f\left( {ax + b} \right)dx} = {\large\frac{1}{a}\normalsize} F\left( {ax + b} \right) + C\)

Таблица интегралов

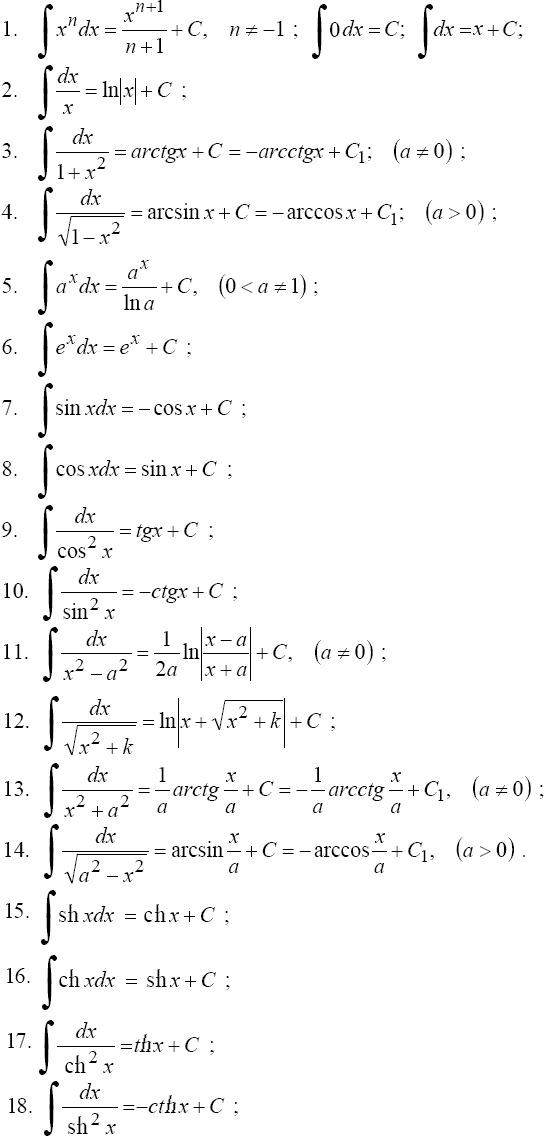
Пример 1. Вычислить: \(\int {\left( {\sqrt x + \sqrt[\large 3\normalsize]{x}} \right)dx}\).

Решение:

\({\int {\left( {\sqrt x + \sqrt[\large 3\normalsize]{x}} \right)dx} } = {\int {\sqrt x dx} + \int {\sqrt[\large 3\normalsize]{x}dx} } = {\int {{x^{\large\frac{1}{2}\normalsize}}dx} + \int {{x^{\large\frac{1}{3}\normalsize}}dx} }= \\= {\frac{{{x^{\large\frac{1}{2}\normalsize + 1}}}}{{\frac{1}{2} + 1}} + \frac{{{x^{\large\frac{1}{3}\normalsize + 1}}}}{{\frac{1}{3} + 1}} + C }= {\frac{{2{x^{\large\frac{3}{2}\normalsize}}}}{3} + \frac{{3{x^{\large\frac{4}{3}\normalsize}}}}{4} } = {\frac{{2\sqrt {{x^3}} }}{3} + \frac{{3\sqrt[\large 3\normalsize]{{{x^4}}}}}{4} + C.}\)

Методы интегрирования

1. Непосредственное интегрирование

Вычисление интегралов с помощью непосредственного использования таблицы простейших интегралов и основных свойств неопределенных интегралов называется непосредственным интегрированием.

2. Подведение под знак дифференциала

Данный метод эквивалентен методу замены переменной. В формуле неопределенного интеграла величина \(dx\) означает, что берется дифференциал от переменной \(x\).

Можно использовать некоторые свойства дифференциала, чтобы, усложнив выражение под знаком дифференциала, тем самым упростить нахождение самого интеграла. Для этого используется формула \(y'(x)dx=dy(x)\). Необходимо иметь в виду простейшие преобразования дифференциала:

\(1) \ dx=d(x+b), b=const \\2) \ dx=\frac1{a}d(ax+b), a=const\ne0 \\3) \ xdx=\frac12d(x^2+b) \\4) \ sinxdx=-d(cosx) \\5) \ cosxdx=d(sinx)\)

Пример 2. Вычислить: \(\int sin^2x\cdot cosxdx\).

Решение: \(\int sin^2x\cdot cosxdx=\int sin^2x\ d(sinx)=\frac{sin^3x}3+C\).

3. Метод подстановки

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки).

Пусть требуется вычислить интеграл \(\int F(x)dx\). Сделаем подстановку \(x=\varphi(t), \ где \ \varphi(t)\) – функция, имеющая непрерывную производную. Тогда \(dx=\varphi '(t)\cdot dt\) и на основании свойства инвариантности формулы интегрирования неопределенного интеграла получаем формулу интегрирования подстановкой: \(\int F(x)dx=\int F(\varphi(t))\cdot \varphi'(t)dt\).

Пример 3. Вычислить: \(\int\frac{dx}{x+\sqrt{x}}\).

Решение: Возьмем \(x=t^2, тогда \ dx=2tdt\).

\(\int\frac{dx}{x+\sqrt{x}} \Rightarrow \int\frac{2tdt}{t^2+t}=2\int\frac{dt}{t+1}=2ln|t+1|+C=2ln|\sqrt{x}+1|+C\).

4. Интегрирование по частям

Интегрированием по частям называют интегрирование по формуле \(\int {udv} = uv - \int {vdu} \), где \(u(x), v(x)\) − дифференцируемые функции.

Пример 4. Вычислить: \(\int x\cdot sinxdx\).

Решение: \(x=u, \ sindx=dv \Rightarrow du=dx, \ v=-cosx\).

\(\int x\cdot sinxdx=x\cdot(-cosx)-\int(-cosx)dx=-xcosx+sinx+C\).