Перпендикуляр и наклонная. Расстояние от прямой до плоскости

Перпендикуляром, опущенным из данной точки на данную плоскость, называется отрезок, соединяющий данную точку с точкой плоскости и лежащий на прямой, перпендикулярной плоскости. Конец этого отрезка, лежащий в плоскости, называется основанием перпендикуляра.

Расстоянием от точки до плоскости называется длина перпендикуляра, опущенного из этой точки на плоскость.

Наклонной, проведенной из данной точки к данной плоскости, называется любой отрезок, соединяющий данную точку с точкой плоскости, не являющийся перпендикуляром к плоскости. Конец отрезка, лежащий в плоскости, называется основанием наклонной. Отрезок, соединяющий основания перпендикуляра наклонной, проведенных из одной и той же точки, называется проекцией наклонной.

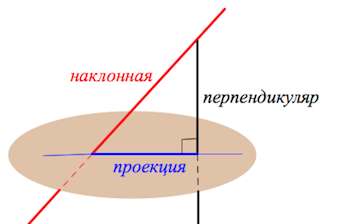
AB – перпендикуляр к плоскости α. AC – наклонная, CB – проекция. С – основание наклонной, B – основание перпендикуляра.

У равных наклонных, проведенных к плоскости из одной точки, проекции равны.

Из двух наклонных, проведенных к плоскости из одной точки, больше та, у которой проекция больше.

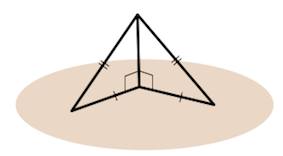
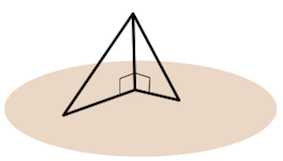
Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна ее проекции, то она перпендикулярна и самой наклонной.

Обратная теорема. Если прямая на плоскости перпендикулярна наклонной, то она перпендикулярна и проекции наклонной.

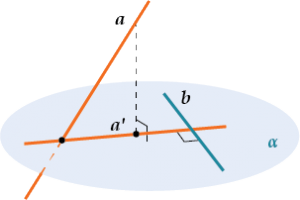
Прямая a, не лежащая в плоскости α, перпендикулярна прямой b, лежащей в плоскости α, тогда и только тогда, когда проекция a'​​ прямой a перпендикулярна прямой b.

Пример. От­ре­зок SО – пер­пен­ди­ку­ляр к плос­ко­сти квад­ра­та АВСD, где точка О – центр квад­ра­та. До­ка­зать: \(BD \perp SC\).

До­ка­за­тель­ство:

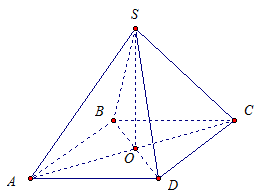
Пер­вый спо­соб.

Имеем квад­рат, центр квад­ра­та точка – О, SО – пер­пен­ди­ку­ляр. Зна­чит, для на­клон­ной SC от­ре­зок ОС есть про­ек­ция.

Пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой ОС, ко­то­рая яв­ля­ет­ся про­ек­ци­ей на­клон­ной SC, зна­чит, по тео­ре­ме о трех пер­пен­ди­ку­ля­рах, пря­мая ВD пер­пен­ди­ку­ляр­на на­клон­ной SC.

Вто­рой спо­соб.

Пря­мая SО пер­пен­ди­ку­ляр­на плос­ко­сти АВС, а зна­чит – и пря­мой ВD, ле­жа­щей в ней.

Пря­мая ВD пер­пен­ди­ку­ляр­на SО и пря­мая ВD пер­пен­ди­ку­ляр­на пря­мой АС по свой­ству квад­ра­та.

По­лу­ча­ем, что пря­мая ВD пер­пен­ди­ку­ляр­на двум пе­ре­се­ка­ю­щим­ся пря­мым плос­ко­сти SОС, зна­чит, она пер­пен­ди­ку­ляр­на ко всей плос­ко­сти SОС, а зна­чит – и к пря­мой SC, ле­жа­щей в этой плос­ко­сти.

Расстояние от точки до плоскости есть перпендикуляр, опущенный на эту плоскость, то есть расстояние от точки А до плоскости a, есть длина перпендикуляра АВ.

1. Если прямая параллельна плоскости, то расстояние от произвольной точки прямой до плоскости называется расстоянием между прямой и параллельной ей плоскостью.
2. Если две плоскости параллельны, то расстояние от произвольной точки одной из плоскостей до другой называется расстоянием между данными плоскостями.
3. Если две прямые скрещиваются, то расстояние между одной из этих прямых и плоскостью, проведенной через другую прямую параллельно первой, называется расстоянием между скрещивающимися прямыми.