Наибольшее и наименьшее значение функций на промежутке

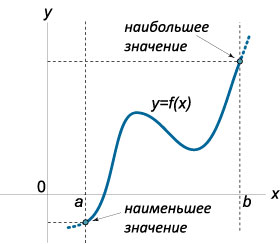
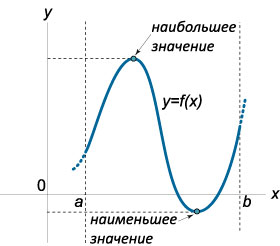
Если функция \(y=f(x)\) определена и непрерывна на отрезке \([a;b]\), то она на этом отрезке достигает своих наибольшего и наименьшего значений. Если свое наибольшее значение \(M\) функция \(f(x)\) принимает в точке \(x_0\in[a;b]\), то \(M=f(x_0)\) будет локальным максимумом функции \(f(x)\), так как в этом случае существует окрестность точки \(x_0\), такая, что \(f(x)\le f(x_0)\).

Однако свое наибольшее значение \(M\) функция \(f(x)\) может принимать и на концах отрезка \([a;b]\). Поэтому, чтобы найти наибольшее значение \(M\), непрерывной на отрезке \([a;b]\), функции \(f(x)\), надо найти все максимумы функции на интервале \((a;b)\) и значения \(f(x)\) на концах отрезка \([a;b]\), то есть \(f(a)\) и \(f(b)\), и выбрать среди них наибольшее. Вместо исследования на максимум можно ограничиться нахождением значений функции в критических точках.

Наименьшим значением \(m\) непрерывной на отрезке \([a;b]\) функции \(f(x)\) будет наименьший минимум среди всех минимумов функции \(f(x)\) на интервале \((a;b)\) и значений \(f(a)\) и \(f(b)\).

Чтобы найти наибольшее или наименьшее значения функции на отрезке, нужно исследовать поведение функции на данном отрезке с помощью производной.

Для этого мы следуем известному алгоритму:

1. Находим ОДЗ функции.
2. Находим производную функции.
3. Приравниваем производную к нулю.
4. Находим промежутки, на которых производная сохраняет знак, и по ним определяем промежутки возрастания и убывания функции: а) если на промежутке I производная функции \(f'(x)>0\), то функция \(y=f(x)\) возрастает на этом промежутке; б) если на промежутке I производная функции \(f'(x)<0\), то функция \(y=f(x)\) убывает на этом промежутке.
5. Находим точки максимума и минимума функции. В точке максимума функции производная меняет знак с «+» на «–». В точке минимума функции производная меняет знак с «–» на «+».
6. Находим значение функции в концах отрезка,

• затем сравниваем значение функции на концах отрезка и в точках максимума, и выбираем из них наибольшее, если нужно найти наибольшее значение функции;
• или сравниваем значение функции на концах отрезка и в точках минимума, и выбираем из них наименьшее, если нужно найти наименьшее значение функции.

Например, рассмотрим функцию \(f(x)=x^3-2x^2+3\). График этой функции выглядит так:

В зависимости от того, на каком промежутке мы будем рассматривать функцию, алгоритм нахождения наибольшего или наименьшего значения будет различным.

1. Рассмотрим функцию на отрезке \(x\in[-1;0]\).

Функция возрастает на этом отрезке, поэтому наибольшее значение она будет принимать в правом конце отрезка: \(f(0)\), а наименьшее – в левом: \(f(-1)\).

2. Рассмотрим функцию на отрезке \(x\in[-1;1]\).

Очевидно, что наибольшее значение функция принимает в точке максимума \(f(0)\), а наименьшее – в одном из концов отрезка, то есть надо найти значения \(f(-1)\) и \(f(1)\) и выбрать из них наименьшее.

3. Если мы рассмотрим функцию на отрезке \(x\in[-1;2]\), то, чтобы найти наибольшее значение, нам нужно будет сравнить значения функции в точке максимума и на правом конце отрезка, то есть \(f(0)\) и \(f(2)\).

Чтобы найти наименьшее значение функции, нам нужно будет сравнить значения функции в точке минимума и на левом конце отрезка, то есть \(f(\frac43)\) и \(f(-1)\).

Эти рассуждения очевидны, если перед глазами есть график функции. Но эскиз графика легко нарисовать, проведя исследование функции с помощью производной:

1. ОДЗ функции \(f(x)=x^3-2x^2+3\) – множество действительных чисел.

2. \(f'(x)=3x^2-4x\).

3. \(3x^2-4x=0 \Rightarrow x_1=0, x_2=\frac43\).

Нанесем корни производной на числовую ось и расставим знаки. Теперь поведение функции легко определить, и, следуя за стрелками, символизирующими возрастание – убывание, можно схематично изобразить ее график:

Пример 2. Найти наибольшее и наименьшее значения функции на заданном отрезке: \(f\left( x \right) = {x^2} - 2x + 5,\;\;x \in \left[ { - 1;4} \right]\).

Решение: Данная функция определена и дифференцируема при всех \(x\in \mathbb R\). Определим стационарные точки:

\({f'\left( x \right) = 0,}\;\; {\Rightarrow {\left( {{x^2} - 2x + 5} \right)^\prime } = 0,}\;\; {\Rightarrow 2x - 2 = 0,}\;\; {\Rightarrow x = 1}\).

Найденная точка локального экстремума принадлежит интервалу \((−1;4)\). Вычислим значения функции в точке \(x=1\) и на концах отрезка:

\({f\left( 1 \right) = {1^2} - 2 \cdot 1 + 5 = 4,}\;\;\; {f\left( { - 1} \right) = {\left( { - 1} \right)^2} - 2 \cdot \left( { - 1} \right) + 5 = 8,}\;\;\; \\ {f\left( 4 \right) = {4^2} - 2 \cdot 4 + 5 = 13}.\)

Следовательно, наибольшее значение функции равно \(f(4)=13\), а наименьшее значение составляет \(f(1)=4\).