+7 (727) 344 95 95
Сдать пробный ЕНТ
Русский

Скачай приложение iTest

Готовься к школьным экзаменам в более удобном формате

logo-device logotype logotype-float

Площади поверхности тел
Предыдущий конспект Следующий конспект
Конспект

Площадь поверхности многогранника равна сумме площадей его граней.

Призма

призма

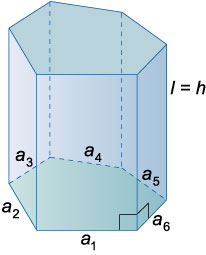
Площадь боковой поверхности правильной призмы: \({S_{\text{бок}}} = {P_{\text{осн}}}\ell = \left( {{a_1} + {a_2} + \ldots + {a_n}} \right)\ell\), где \({P_{\text{осн}}}\) − периметр основания призмы, \({a_1},{a_2}, \ldots ,{a_n}\) − стороны основания, \(\ell\) − длина бокового ребра (в прямой призме боковое ребро совпадает с высотой \(h\)).

Площадь боковой поверхности наклонной призмы: \({S_{\text{бок}}} = p\ell\), где \(p\) − полупериметр перпендикулярного сечения призмы, \(ℓ\) − боковое ребро.

Площадь полной поверхности призмы: \({S_{\text{полн}}} = 2{S_{\text{осн}}}+{S_{\text{бок}}}\).

Параллелепипед

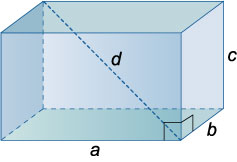
прямоугольный параллелепипед

Площадь полной поверхности прямоугольного параллелепипеда: \(S = 2\left( {ab + ac + bc} \right)\).

Куб

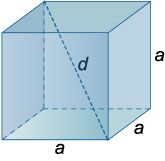
куб - трехмерное тело, каждая из шести граней которого является квадратом

Площадь полной поверхности куба: \(S = 6{a^2}\).

Пирамида

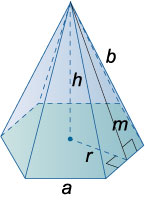
правильная пирамида

Площадь боковой поверхности правильной пирамиды: \({S_{\text{бок}}} = \large\frac{1}{2}\normalsize man = \large\frac{1}{4}\normalsize an\sqrt {4{b^2} - {a^2}} = pm\).

Площадь основания правильной пирамиды: \({S_{\text{осн}}} = pr\), где \(p\) − полупериметр многоугольника в основании, \(r\) − радиус вписанной окружности.

Площадь полной поверхности: \(S = {S_{\text{осн}}} + {S_{\text{бок}}}\).

Усеченная пирамида

усеченная пирамида

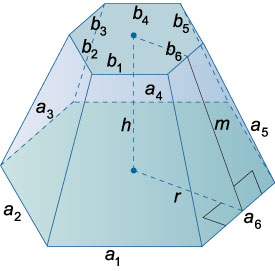
Площадь боковой поверхности правильной усеченной пирамиды: \({S_{\text{бок}}} = m\frac{{{P_1} + {P_2}}}{2}\normalsize\), где \(m\) − апофема (высота боковой грани), \(P_1, P_2\) − периметры верхнего и нижнего оснований.

Площадь полной поверхности: \(S = {S_{\text{бок}}} + {S_1} + {S_2}\).

Тетраэдр

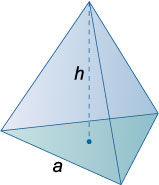
правильный тетраэдр

Площадь основания правильного тетраэдра: \({S_{\text{осн}}} = \large\frac{{{a^2}\sqrt 3 }}{4}\normalsize\).

Площадь полной поверхности правильного тетраэдра: \(S = {a^2}\sqrt 3\).



Вопросы

  1. Высота правильной треугольной пирамиды 4 см, а ее апофемы 8 см. Вычислите площадь боковой поверхности пирамиды.

Сообщить об ошибке