
Скачай приложение iTest
Готовься к школьным экзаменам в более удобном формате
Объемы многогранников
Призма
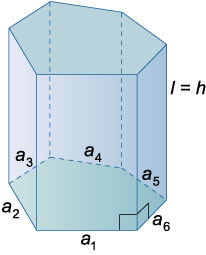
Объем призмы: \(V = {S_{\text{осн}}}h = {S_{\text{сеч}}}\ell\), где \(S_{осн}\) − площадь основания, \(h\) − высота призмы, \(S_{сеч}\) − площадь перпендикулярного сечения, \(ℓ\) − боковое ребро призмы.
Параллелепипед
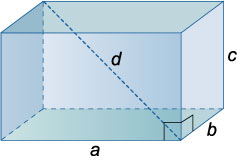
Объем прямоугольного параллелепипеда: \(V = abc\).
Куб
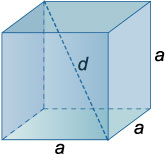
Объем куба: \(V = {a^3}\).
Пирамида
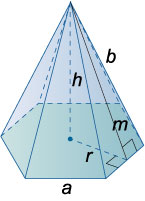
Объем произвольной пирамиды: \(V = \large\frac{1}{3}\normalsize{S_{\text{осн}}}h\).
Объем правильной пирамиды: \(V = \large\frac{1}{3}\normalsize prh\).
Усеченная пирамида
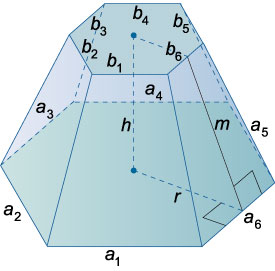
Объем усеченной пирамиды: \(V = \large\frac{h}{3}\normalsize\left( {{S_1} + \sqrt {{S_1}{S_2}} + {S_2}} \right)\).
Тетраэдр
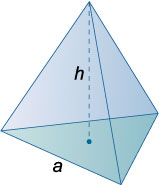
Объем правильного тетраэдра: \(V = \large\frac{1}{3}\normalsize{S_{\text{осн}}}h = \large\frac{{{a^2}}}{{6\sqrt 2 }}\normalsize\).
-
Объем параллелепипеда равен \(9 \ см^3\). Найдите объем треугольной пирамиды \(ABDA_1.\)
-
У правильной треугольной пирамиды объем равен \(72 \;см^3,\) а сторона основания – \(6\;см.\) Определите высоту пирамиды.
-
\(\)У правильной четырехугольной пирамиды объем равен \(168\;см^3 ,\) а площадь круга, вписанного в основание, равна \(9\pi\;см^2. \) Определите высоту пирамиды.
-
Вычислите объем правильной шестиугольной пирамиды с высотой, равной 10\(\sqrt3\) см, и стороной основания, равной 10 см.





